Einer der frühen Pioniere der Computerkartographie ist Prof. Waldo Tobler, University of California, Santa Barbara. Aus dem Jahr 1964 datiert der Aufsatz Geographical Coordinate Computations Part II (Finite Map Distortions). Dept. of the Navy, Office of Naval Reseacrch, Washington D. C. 1964. (= 1964.8) Auf Seite 15 findet sich folgende bemerkenswerte Abbildung:
Die Mercator-Sanson-Projektion in 9 verschiedenen Langen · 9 aspects of the sinusoidal projection
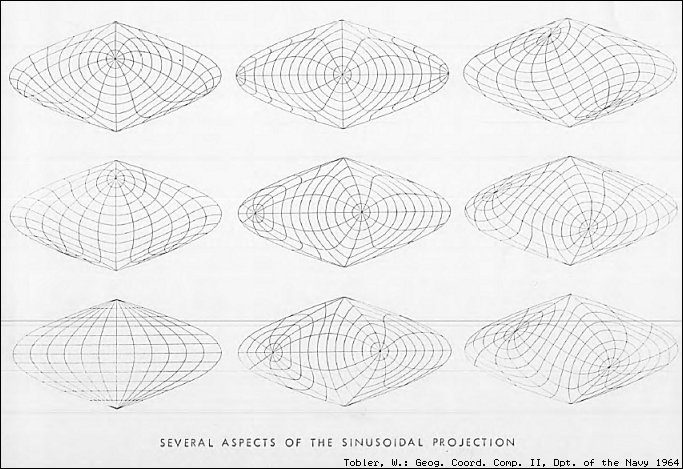
Was für neuartige Erdbilder mögen sich hinter diesen Kartennetzen in schiefachsiger Lage verbergen? Allerdings hat Tobler lediglich die leeren Gitternetze ausgeplottet. Es ist nicht bekannt, ob jemals der Versuch unternommen worden ist, die Karten mit Inhalten vollständig auszuarbeiten. Versuchen wir es also einmal ...
Let us try to generate these projections with a map content ...
Die Netze entstehen, indem man die Erdkugel zunächst auf sich selbst abgebildet, wobei man den Pol ein Stück wandern lässt. Damit wird der Pol zu einem Meta-Pol. Der Mathematiker wird bemerken, dass eine solche Abbildung drei Freiheitsgrade hat. Zunächst lassen sich je eine geographische Länge und Breite des Meta-Poles wählen. Hinzu kommt weiterhin eine Rotation, die z. B. um neue Erdachse ausgeführt werden kann. Wir klassifizieren die schiefen Lagen nach Wray (1974), zitiert nach Canters: Small-scale Map Projection Design 2002, p. 75ff.
Der Maßstab der Karten dierser Seite beträgt 1:400000 (bei 254 dpi) · The maps here are generated in scale 1:400000 (resolution 254 dpi).
Indem nun die Pole unter Beibehaltung des Mittelmeridians auf 30 ° N rotiert werden, gerät Mutter Erde in eine Simple oblique Lage.
Simple oblique I: Meta-pole on 30 ° N, 0° E.
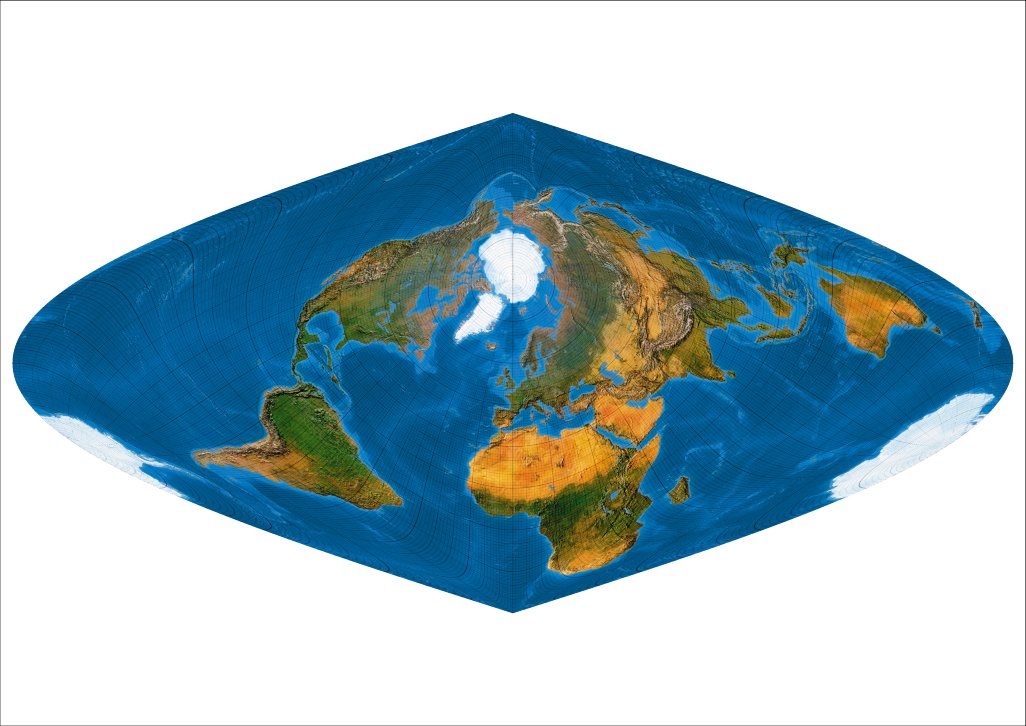
Nanu, 2 Südpole? Das stimmt nicht ganz, wie wir unten bei Entwurf 9 sehen werden.
Nun Rotation (um lediglich 30 °) auf 60 °.
Simple oblique II: Meta-pole on 60 ° N, 0° E.
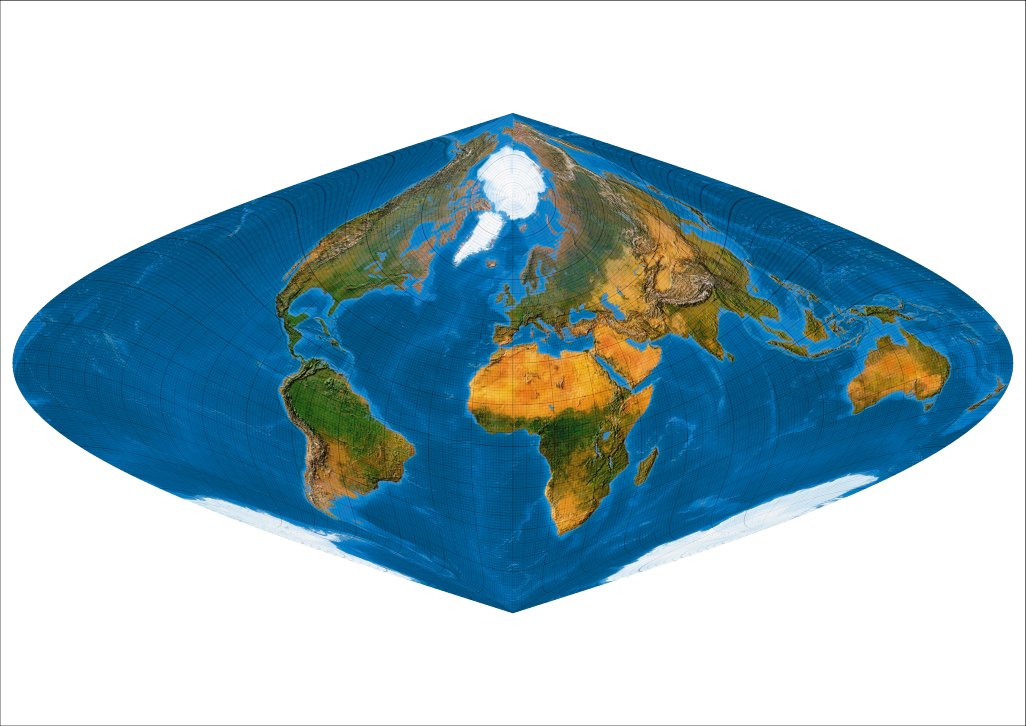
Es entsteht ein interessantes Erdbild, das an an Bartholomew's Nordic Projection erinnert. Auch der Nordic hat vermeintlich 2 Südpole. Vorteilhafte Abbildung der gesamten Landmasse der Erde.
Keine Rotation, Norden oben: Unser gewohntes Erdbild.
Normal: Meta-pole on 90 ° N, 0° E.
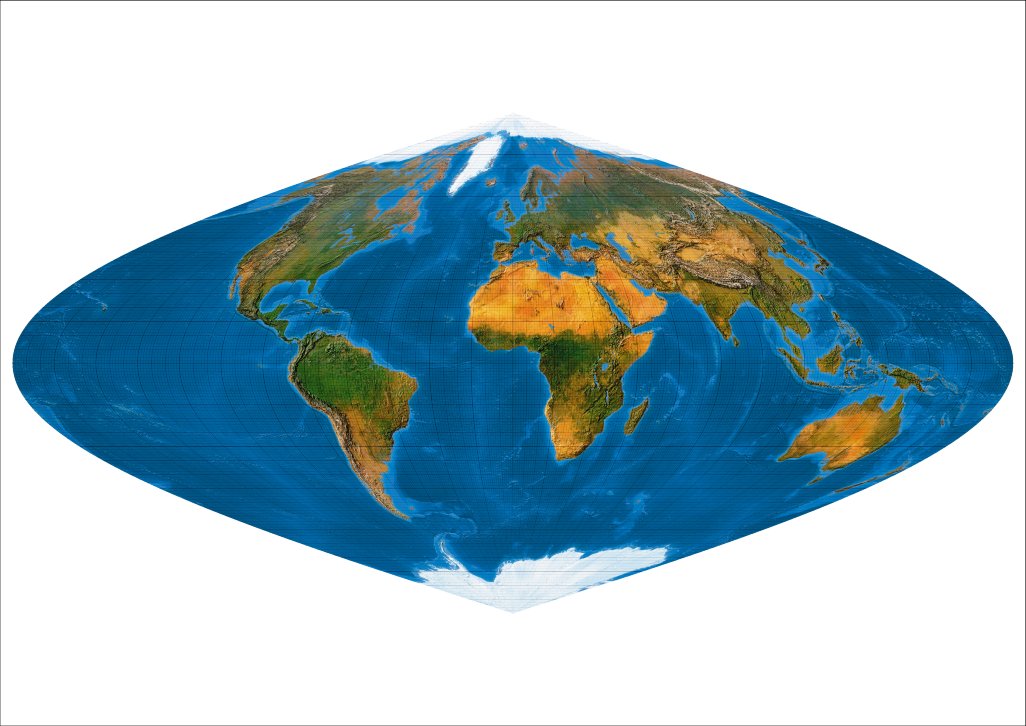
Der gewöhnliche Mercator-Sanson-Entwurf, wie wir ihn kennen. Starke Formverzerrungen in den Außenbereichen.
Eine Verdrehung der Erde um exakt 90 ° bezeichnet Wray, sofern der Pol den Greenwichmeridian entlangwandert, als First transverse.
First transverse: Meta-pole at 90 ° N, 0° E.
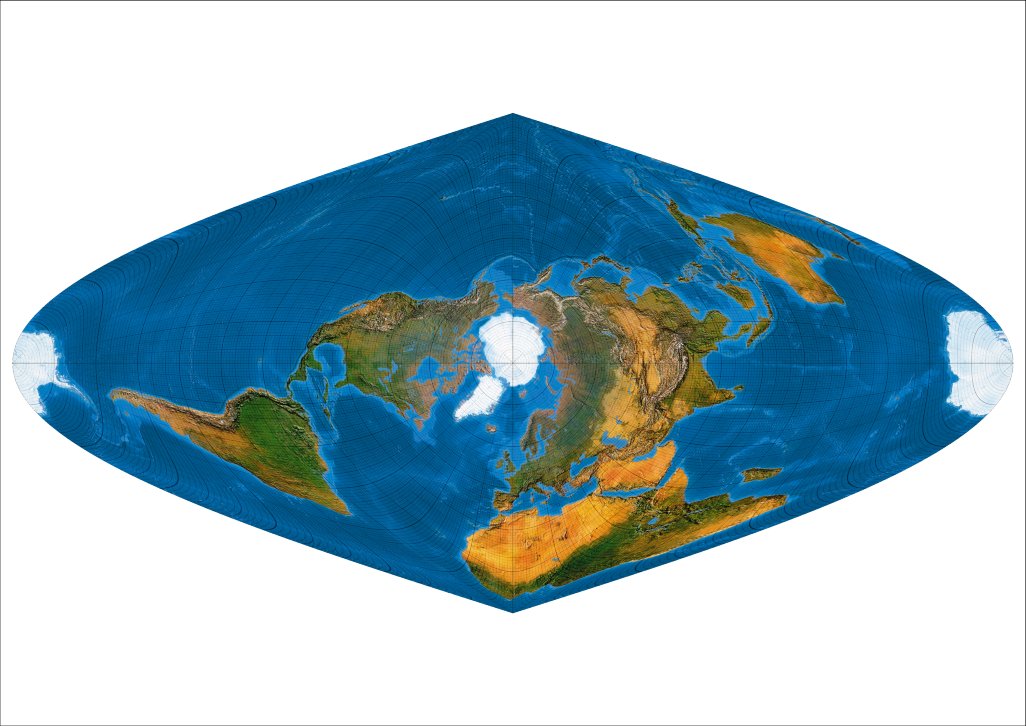
Das Weltbild der Eskimos mit dem Nordpol als Erdmittelpunkt.
(Anmerkung: Für den Wrayschen „Second transverse", bei dem die Metapole auf dem Äquator auf 90 ° (E/W) zu liegen kommen, gibt es kein Toblersches Beispiel.)
Lagen, bei denen der Metapol auf dem Äquator liegt, heißen nach Wray „Transverse oblique“. Metapol auf 0 °N und 30 ° E.
Transverse oblique I: Meta-pole at 0 ° N, 30° E.
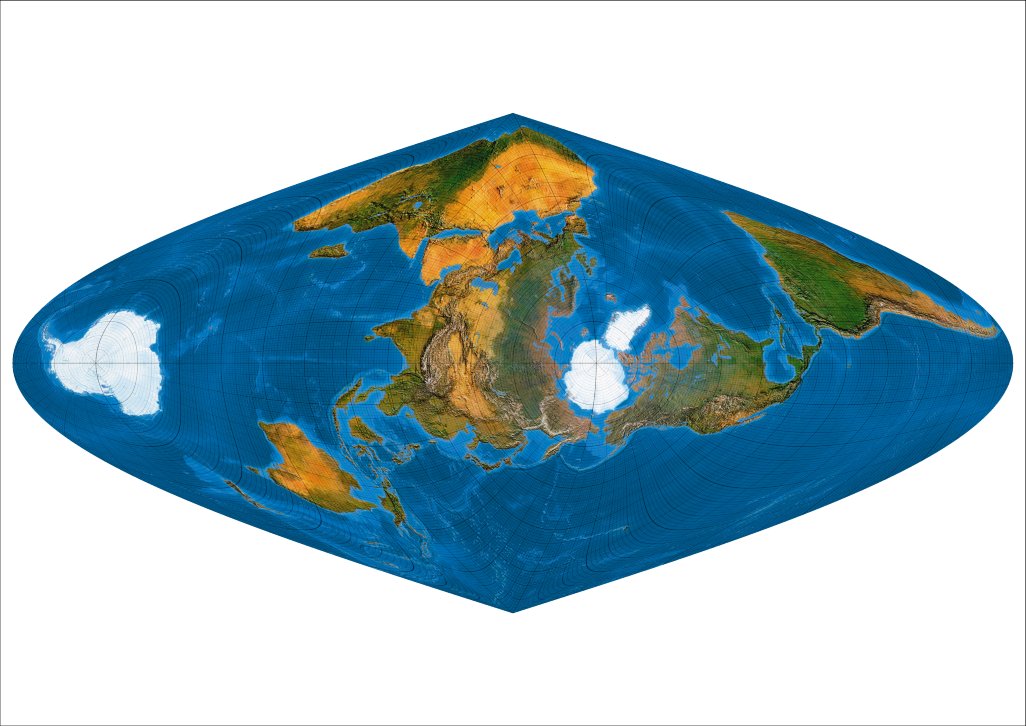
Eine andere Variante: Metapol auf 0 °N und 60 ° E.
Transverse oblique II: Meta-pole at 0 ° N, 60° E.
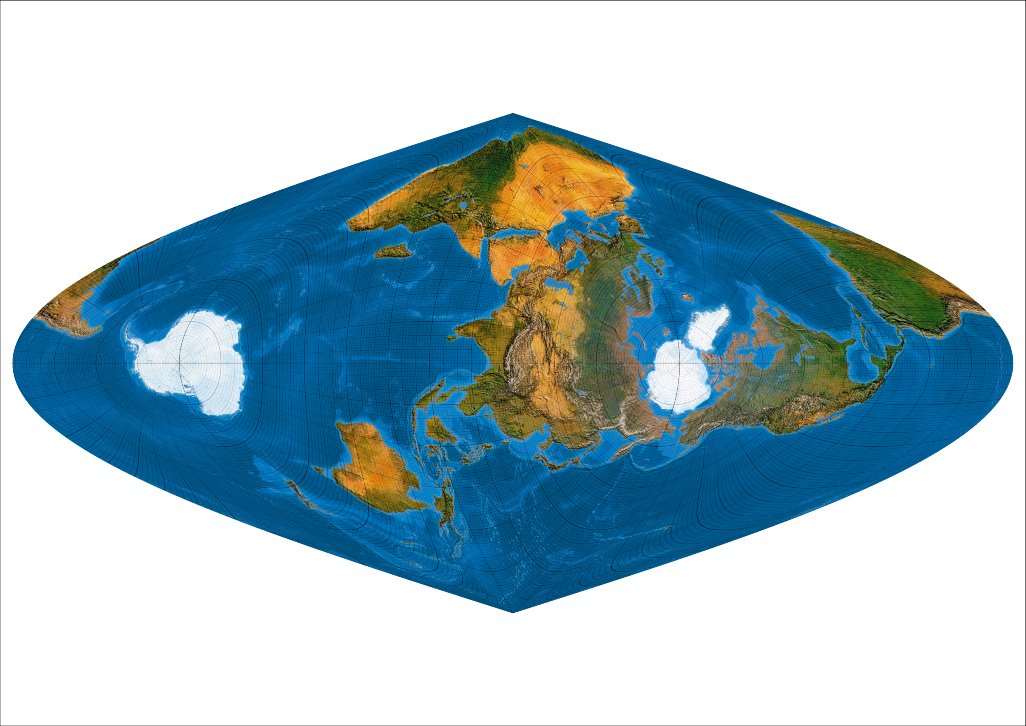
So wird China allmählich zum Reich der Mitte.
Die dritte Toblersche Spalte enthält völlig schiefe Netzbilder, bei denen der Metapol weder auf dem Mittelmeridian, noch auf dem Äquator liegt. Metapol auf 60 °N und 180 ° E, anschließend Verdrehung um 30 °.
Plagal I: Meta-pole at 60 ° N, 180° E, Rotation 30°.
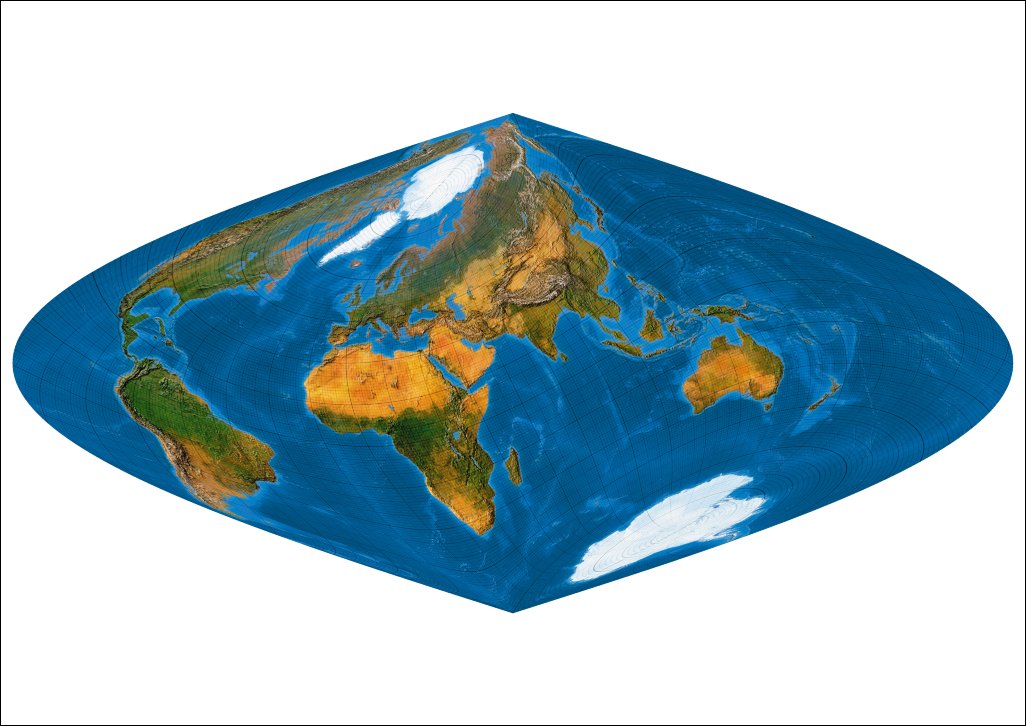
Metapol auf 30 °N und 180 ° E, anschließend Verdrehung um 30 °.
Plagal II: Meta-pole at 30 ° N, 180° E, Rotation 30°.
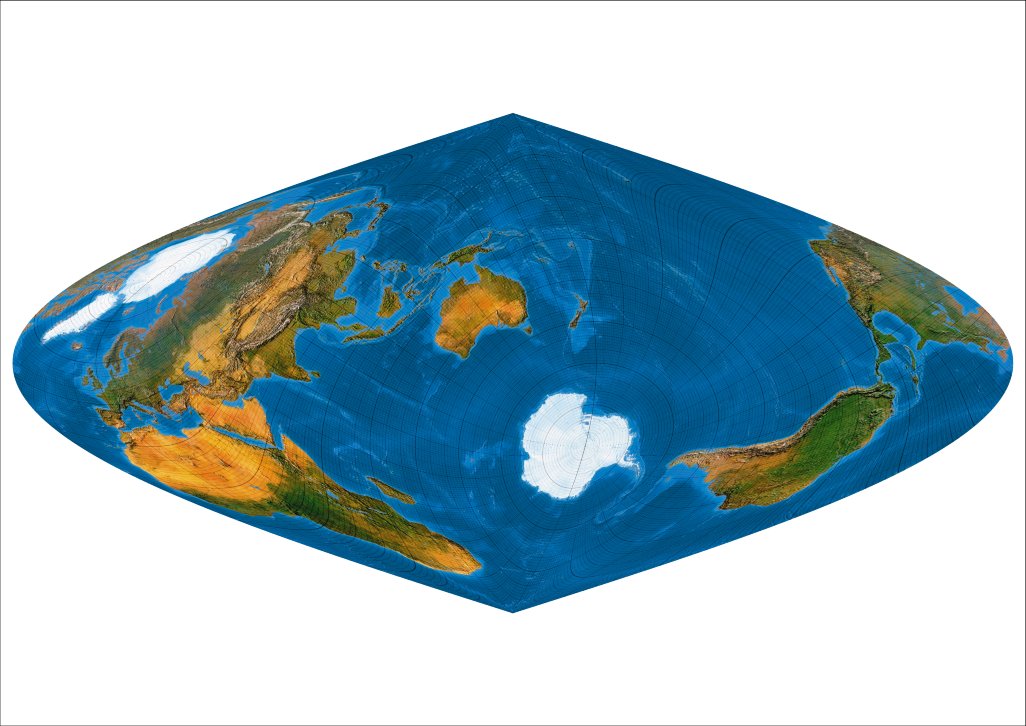
Metapol auf 30 °N und 180 ° E, anschließend Verdrehung um 30 °.
Plagal III: Meta-pole at 60 ° N, 180° E, Rotation 60°.
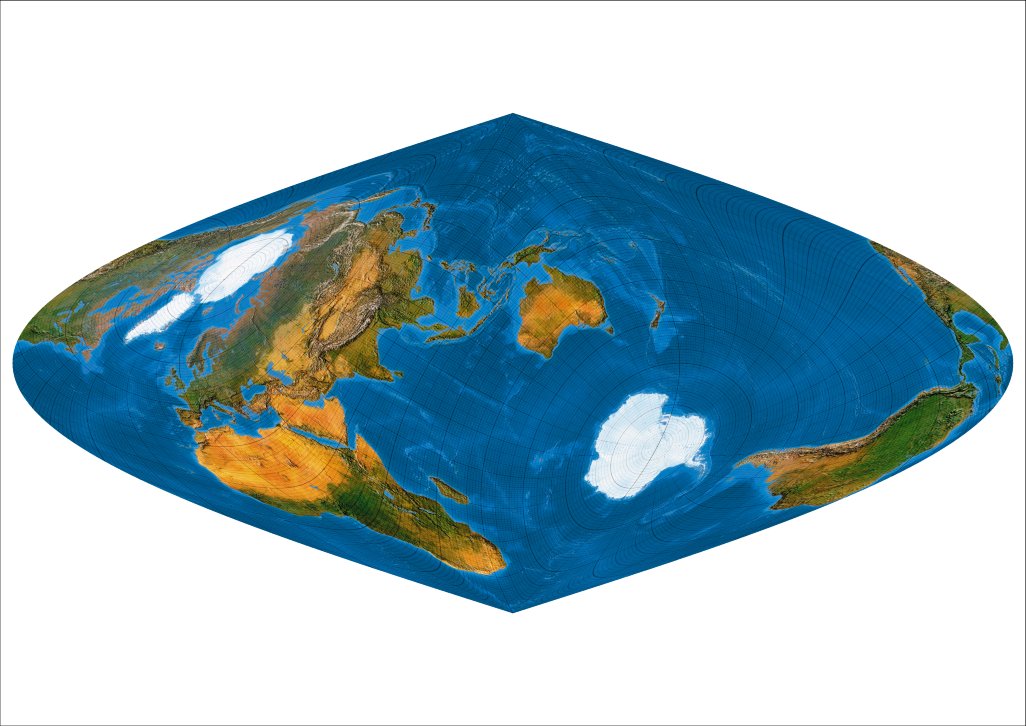
Die Kartenaußenrandlinie ist ein Meridian und schneidet Nordamerika glatt durch: Wenn man das Kartenbild links verlässt, tritt man rechts wieder ein. So klärt sich auch das vermeintlich doppelte Südpolargebiet von Abb. 1 und 2. Die Antarktis wird nicht doppelt abgebildet, sondern nur in zwei Teile zerschnitten.
Assemblerprogramme mit denen die Netzentwürfe gerechnet wurden:
Metatransformation der Erde auf sich selbst (Metatransformation)
Der gute alte Mercator-Sanson
Wichtig: Die Metatransformation projiziert nicht Erdkugel auf Kartenebene, sondern Kugel auf Kugel. Bei der Transformation mit dem Programm Vimage muss daher die Ziegeometrie ein Erdbild sein. Vorgehensweise: Option Zielgeometriewahl auf 2 stellen und das Erdbild in den Sekundäroperanden schaffen. Dessen Geometrie bestimmt dann die Geometrie des Zielbildes.
Ich bedanke mich bei Prof. Waldo Tobler, Geography Departement, University of California.
Many thanks to Prof. Waldo Tobler, Geography Departement, University of California.