1912 – 2012. Geburtstagsbilder für eine Hundertjährige.
 [Gauß-Krüger 1912]
[Gauß-Krüger 1912]
Zurück zur Kartennetzentwurfs-Hauptseite
Gauß-Krüger-Projektion II (Fehleranalyseseite)
Die Königin der Kartennetzentwürfe
Die Gauß-Krüger-Projektion einmal ganz anders.
Die Königin der Kartennetzentwürfe ist die Gauß-Krüger-Projektion. Immer wenn in unseren GPS' etwas mit UTM, WGS84, ED50, Besselellipsoid, Krassowski, Streifennummer, Hochwert, Grad, Minuten und Sekunden nicht hinhaut — dann muss man eben so fix einmal – eine Gauß-Krüger-Projektion rechnen.
Aber nur ganz wenige Menschen – z. B. Wilfried Korth in Potsdam und Friedrich Krumm in Stuttgart (die ich beide sehr verehre) – wissen, was sich dahinter eigentlich verbirgt. Die Gauß-Krüger-Projektion ist die wichtigste Kartenprojektion überhaupt. In ihr werden sehr viele Landeskartenwerke der Welt abgebildet und auch bei der „GPS-Abbildung“ UTM, handelt es sich (abgesehen von einem Faktor 0,9996) um eine waschechte Gauß-Krüger-Projektion.
Das Netz hat Geburtstag. Vor genau 100 Jahren, 1912, veröffentlichte Johann Heinrich Louis Krüger, stellvertretender Abteilungsvorsteher im Kgl. Preuß. Geod. Inst. Berlin in seiner Abhandlung Konforme Abbbildung des Erdellipsoides in der Ebene erstmalig die Formeln (PDF, 6 MByte). 1923 wurde das „Gauß-Krüger-Gitter“ im Reichsamt für Landesaufnahme eingeführt und von dort aus eroberte es sich die Vermessungsverwaltungen vieler Länder der Erde.
Das Jubiläum ist uns Anlass, für diese Themenseite.
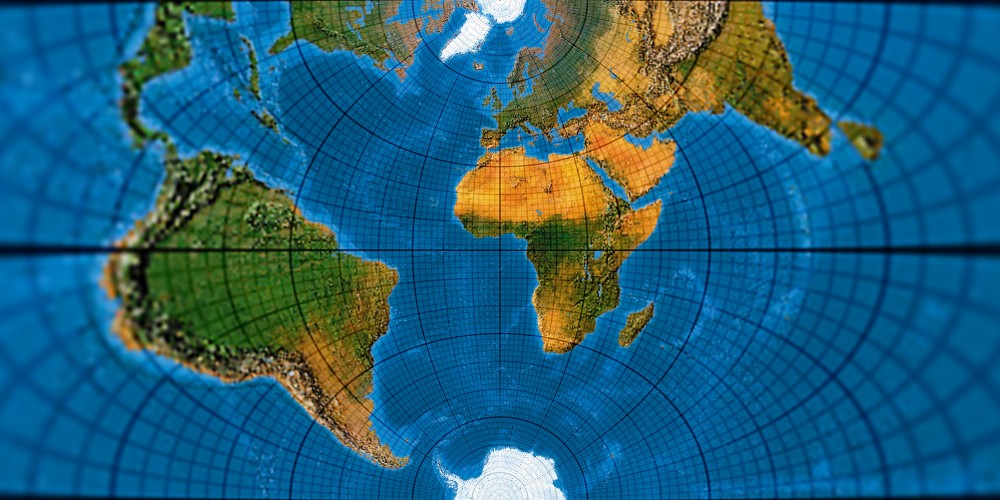
Das Grundprinzip ist einfach. Im Kern ist der Gauß-Krüger ein querachsiger winkeltreuer Zylinderentwurf. Kurze Erläuterung: Erde als Globus mit Nordpol oben und Südpol unten vorstellen. Dann einen Zylinder so, dass die Zylinderachse in der Äquatorebene liegt, um den Globus herumstülpen. Die Erde wird nun den Zylinder in einem Meridiankreis (also in einer über beide Pole laufenden Längengradlinie) berühren. Diese Linie wird nun genau 1:1 von der Erde auf den Zylinder übernommen. Für die übrige Erdfläche fordern wir blumig: Winkeltreue. Was immer das auch sein mag, es gibt nur eine einzige Möglichkeit, eine Kugel auf einen Zylinder winkeltreu abzubilden. Den Gauß-Krüger:
Halt! Einspruch!
Das da oben ist doch gar kein Gauß-Krüger. Der ist nämlich auf der Kugel gerechnet. Der „richtige Gauß-Krüger“ bildet jedoch ein Rotationsellipsoid ab. Dazu braucht man respekteinflößende elliptischen Integrale erster Ordnung und ähnlichen mathmatischen Pulverdampfnebel.
Da erschauert der altgediente Landkartenzeichner samt seinem Tuschefass. Denn auch er wurde von kleinauf durch Schule, Prüfungsstress, Wissensüberfrachtung und irreführende Mathe-Lehrbuchtitel (Numerische Mathematik für Anfänger, Viehweg 2004) darauf konditioniert, das ganze Formelzeugs wie eine garstige Dornenhecke zu empfinden.
Das ist schade. Denn dies verschließt uns zugleich den Blick darauf, dass hier und da ein paar wunderschön berankte Märchenschlosstürme aus so Reihenentwicklungen emporlugen.
Willkommen in der Wunderwelt der Reihenentwickungen
Eine Zahl ausrechnen, so etwa wie der Gastwirt dem Gast einen Zechenbetrag berechnet, das ist in der Höheren Geodäsie nicht üblich. Statt dessen ist das Approximiieren mit Potenzreihen in Gebrauch. Oft wird mit einem recht trivialen Anfangswert begonnen, sagen wir, 0 oder 1. Durch schrittweises Hinzuaddieren von Potenzgliedern – hoch 1, 2, 3, 4, 5 usw. – ändert sich jeweils die Gesamtsumme aller Glieder der Reihe. Nun könnte meinen, die Summe wächst ins Zufällige oder Unendliche. Nicht immer. Oft lässt es sich so organisieren, dass die hinzutretende Summanden allmählich immer kleiner werden. Damit werden dann natürlich auch die Änderungen der Gesamtsumme immer winziger. Mit etwas Glück nähert sich die Summer aller Potenzglieder dem gesuchten Zahlenwert immer mehr an. Der Fachjargon spricht hier hier von einer Konvergenz der Reihe „gegen“ ebendiesen Wert. Die Summe, nehme man auch noch so viele Glieder hinzu, wird den Wert zwar niemals erreichen, aber irgendwann liegen wir nur noch ein My daneben. Das reicht dann eben aus und man „bricht ab.“
Ein wunderschönes Beispiel finden wir in einem alten Aufsatz von Herrn Geh. Rat und Ritter Bessel aus dem Jahr 1837:
 Originalveröffentlichung des berühmten Besselschen Ellipsenintegrales *)
Originalveröffentlichung des berühmten Besselschen Ellipsenintegrales *)
(Astronomische Nachrichten Nr. 333, 1837, John G. Wolbach Library/NASA Astrophysics Data System, ca. 1,5 MByte). Das braucht man schon einmal für den Gauß-Krüger. Hat er doch halbwegs durchschaubar aufgeschrieben, oder? Auf jeden Fall, wenn man das mal mit den Formeln vergleicht, die heutzutage so im Weisstein drinnestehen.
Nein, nicht rechnen. Bilder machen —
Karten
Karten können den Pulverdampfnebel lichten und die Dornen zum Blühen zu bringen. Nich soviel Vorrede. Anfangen.
(Gauß-Krüger. Besselellipsoid. Pixelgröße 40×40 Kilometer. Rechenauflösung 100dpcm. Damit Äquatorlänge 10 cm, Maßstab 1:400 Millionen. Zugegeben ein dem Geodäten fremder Maßstabsbereich.)
Wir beginnen arttypisch mit dem allerersten Glied, und erhalten eine allererste Approximation. Fast sieht es ein wenig aus, als wäre die Erde eine Scheibe:
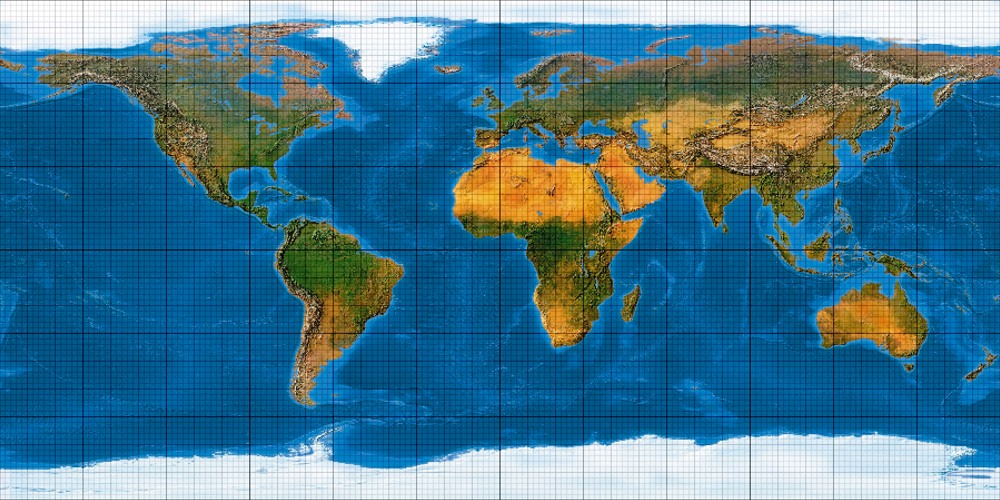
Es ist dies die bekannte abstandstreue Zylinderprojektion oder quadratische Plattkarte.
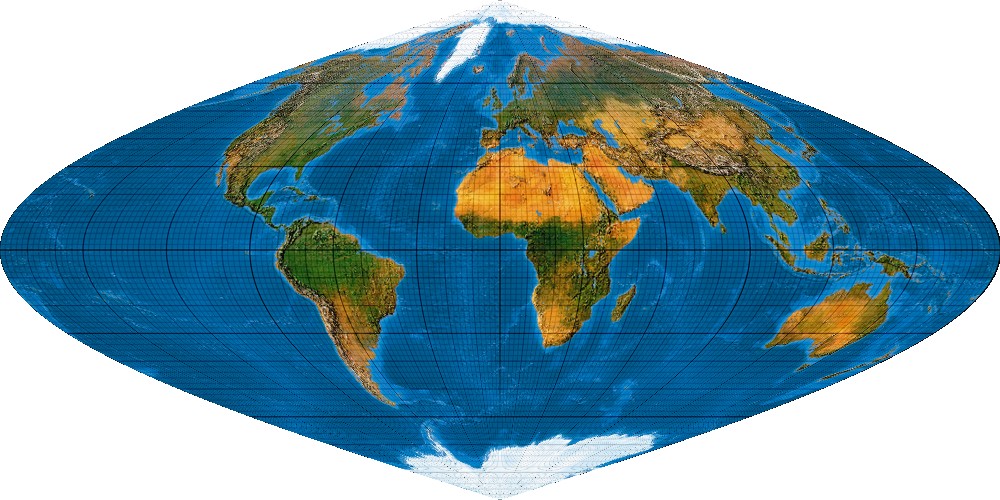
Durch Hinzufügen eines Linearterms, quasi x hoch 1, wird es nun schon etwas weltkartenähnlicher – und, was haben wir denn da? Den guten alten Mercator-Sanson-Entwurf, der sich hier als lineare Approximation der Gauß-Krüger-Projektion entpuppt:
Nun kommt das quadratische Glied. Das sorgt nun dafür, dass unser Netz die Niederungen kartographischer Trivialprojektionen verlässt. Es wird sichtbar „höher mathematischer“:
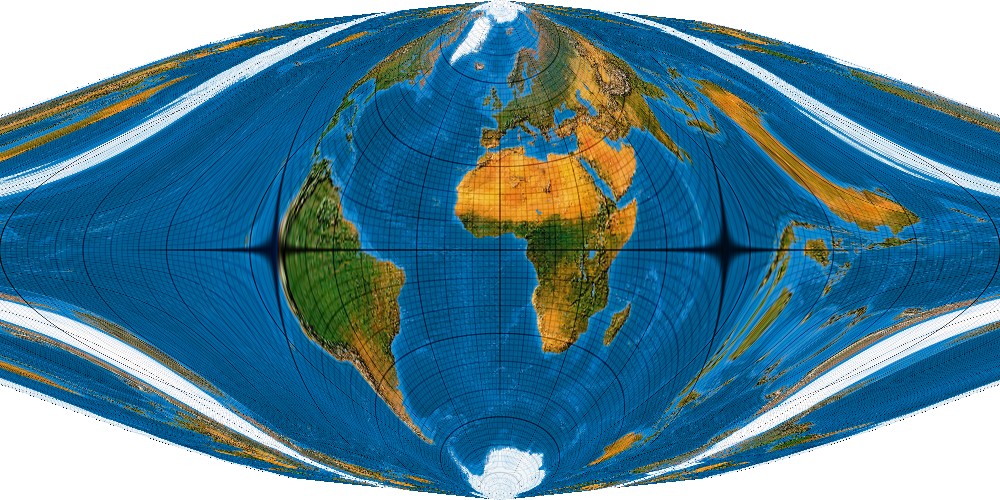
Ein ungewohntes Bild. Und das soll ein Gauß-Krüger sein?
Durchaus. Das Originelle an den hier von uns vorgestellten Bildern ist, dass wir die gesamte Erdoberfläche projizieren, wohingegen übliche geodätische Rechnungen lediglich nur schmale Streifen von etwa 1,5° oder 3° Breite rechts und links des Mittelmeridians (der senkrechten Bildmittelachse) zur Abbildung bringen. Kritische Geister, die hier die typischen Meridian-Zweiecke suchen, seien also auf den zentralen Bildteil verwiesen.
Herr Ober, den nächsten Gang bitte. Die kubische Approximation ...
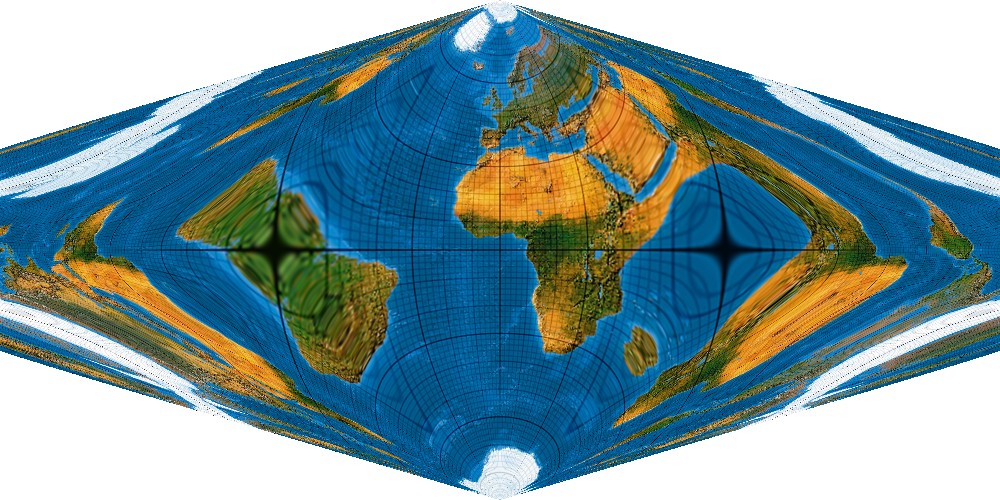
Nun die 4. Potenz, in meinem eigenen Programmierslang mitunter „quadronisch“ genannt. Die Parallelkreise erhalten eine interessante wellenförmige Bewegung ...
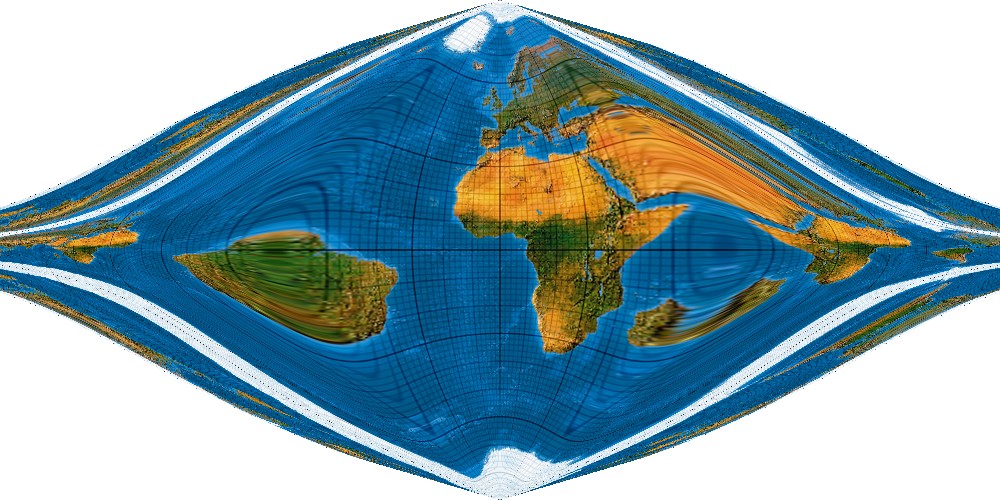
Wir fügen ein Polynom 5. Grades, sozusagen das „quintonische Glied“ hinzu ...
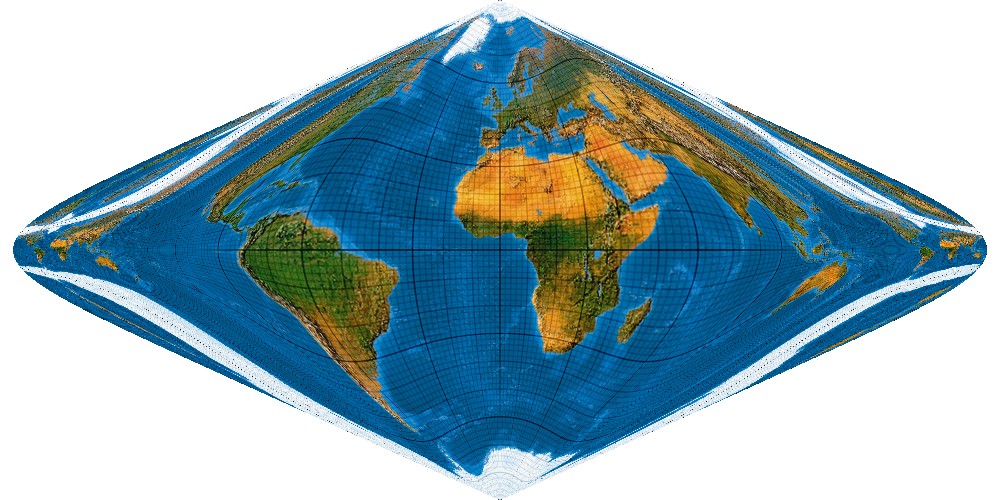
Der 6. Grad ergibt ein wunderschönes Netzbild mit Kugelanmutung im Karteninneren ...
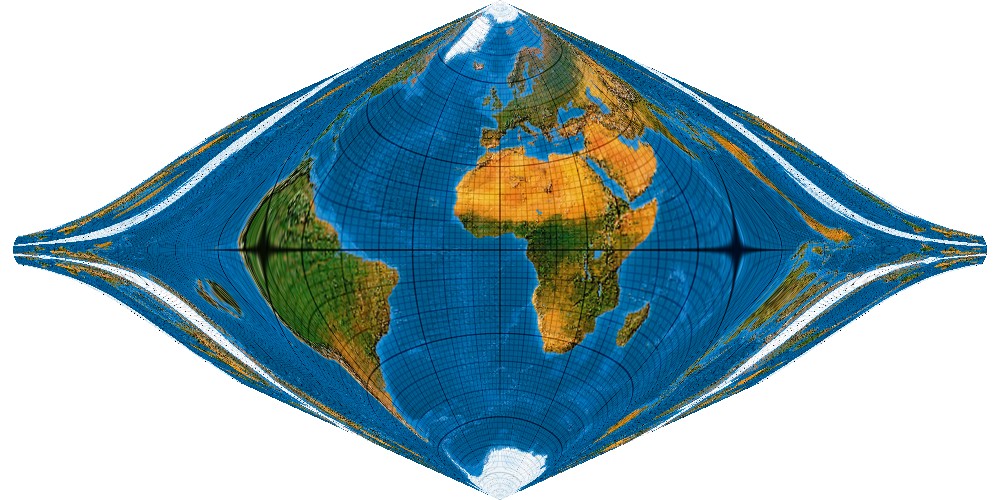
Die 7. Potenz ...
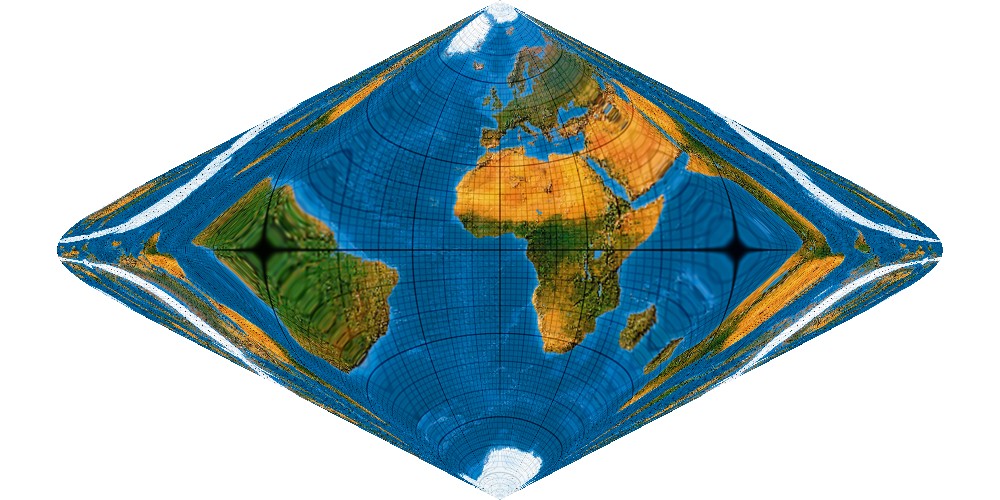
Die 8. Potenz ...
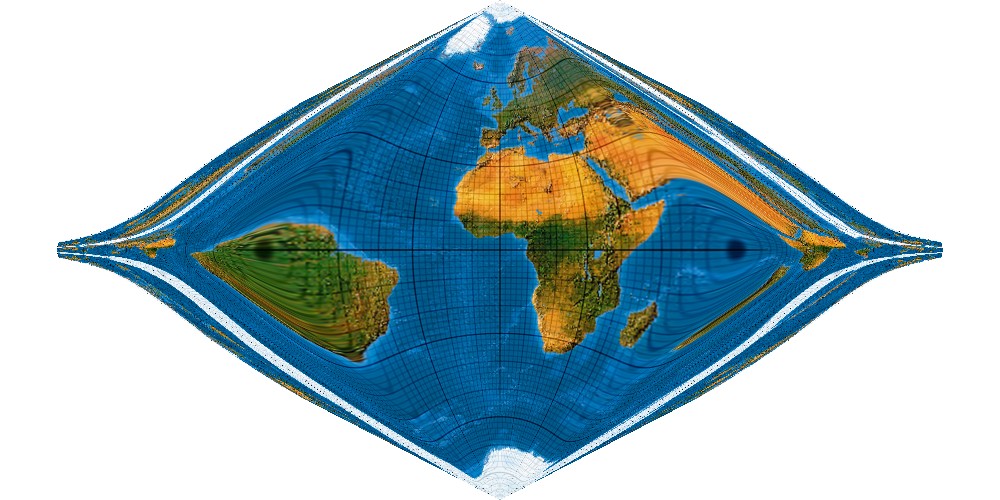
So, das mag ausreichen. Wir brechen ab.
Wenn der Gastwirt mit seinem Rechnungsbetrag nur noch ein paar millionstel Cent neben der Zeche liegt, können wir ihn erlösen. Wir runden auf das nächst höhere Pixel auf. Zahlen!
Was ist da aber mit Südamerika? Auch Grönland und Madagaskar ändern abrupt ihre Form, wenn je ein weiteres Polynomglied hinzutritt. Hat er sich da verrechnet? Natürlich nicht. Es ist vielmehr eine andere Diagnose. Die Reihe konvergiert nicht überall. Außerhalb des Konvergenzbereiches laufen die Gradnetzlinien ins Unendliche weg. Divergenz. Im wahrsten Sinne des Wortes.
Tja, das sind eben die Grenzen einer Reihenentwicklung. Na, oben hatten wir ja ein sphärisches Bild.
Meist werden nur 3 oder 6° rechts und links des Mittelmeridians gerechnet. Wir haben ihn einmal un die ganze Erde herum entwickelt. Der Gauß-Krüger ist die Königin der Kartennetzentwürfe, das Netz der Netze. Kein Pixel in irgendeinem Navi wäre ohne Gauß-Krüger dort, wo es ist. Wir würden uns pausenlos verfahren.
Hut ab vor der Meisterleistung von Carl Friedrich Gauß, den kennen alle — und Johann Heinrich Louis Krüger. Den Prof., den nur wenige kennen. Hat er übrigens mit zehnstelligen Logarithmen gerechnet, der alte Krüger.
Wie vor 100 Jahren.
Jung, Junge, das waren Zeiten.
Zurück zur Kartennetzentwurfs-Hauptseite
Gauß-Krüger-Projektion II (Fehleranalyseseite)
*) Achtung, auch wenn Bessel in diesem Aufsatz Erdabmessungen mitteilt, das ist nicht das Besselellipsoid, sondern sein erstes, das „falsche“ Besselellipsoid. Das „richtige“ Besselellipsoid stammt aus dem Jahr 1841.