 [Abbildung: Wagner S. 33]
[Abbildung: Wagner S. 33]
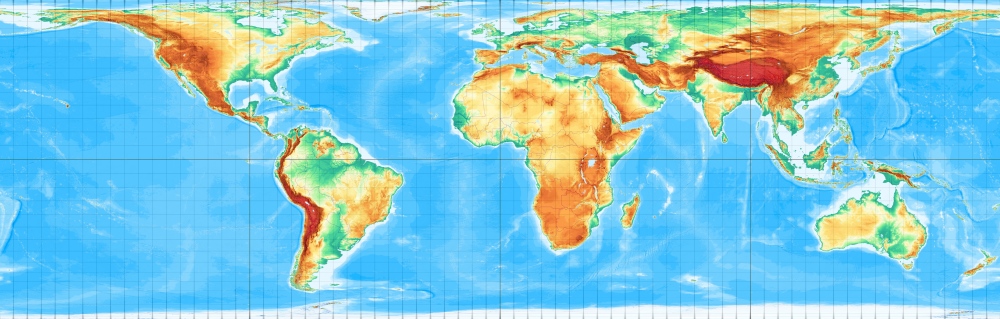
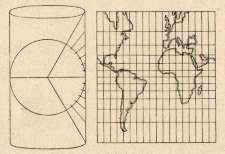
Wenn in einer Karte die Meridiane gleichabständige parallele Linien sind, so hat man einen Zylinderentwurf vorliegen, genauer gesagt, einen Zylinderentwurf in normaler oder polständiger Lage. Hierbei fallen Erd- und Zylinderachse zusammen.
Wenn man nun die Parallelkreise in ihrem Abstand von der Äquatorebene anordnet, ergibt sich folgendes Bild:
Der Entwurf besitzt die Eigenschaft der Flächentreue. Autor, klar, mal wieder Lambert. Besonders schön ist er nicht, und auch nicht besonders praktisch: Die polnahen Gebiete sind sehr stark verzerrt. [Entwurf 8 nach Wagner]
Das Bild bessert sich etwas, wenn der Zylinder die Erde nicht am Äquator berührt, sondern in zwei Parallelkreisen schneidet, hier bei je 40°.
Ein Entwurf, der nicht völlig unbrauchbar ist und für gewisse Aufgaben durchaus eingesetzt werden kann.
Allerdings wurde eine Variante des Netzes als „Peters-Projektion“ 1974 von dem Geographen Arno Peters „neu erfunden“ und als vermeintlich allerbeste Projektion aller Zeiten mit einigem Erfolg empfohlen und publiziert.
Dieses Scharlataneriestück der Kartennetzentwurfslehre hat unter den Kartographen viel Kopfschütteln verursacht dem Ruf des Entwurfes sehr geschadet.
Einfach Meridiane und Parallelkreise in einem Quadratnetz anordnen und man erhält den einfachsten Netzentwurf, den es überhaupt gibt: den abstandstreuen Zylinderentwurf.
Der Entwurf war schon im Altertum bekannt und erlebt als „geographische Projektion“ eine gewisse Computer-Renaissance. Er ist gewissermaßen eine „natürliche Projektion“: X=geographische Länge, Y=geographische Breite. Auch als quadratische Plattkarte bezeichnet. [Nr. 6 im Wagner]
Die quadratische Plattkarte hat ein Geschwisterkind, die rechteckige Plattkarte. Wie bei den flächentreuen Entwürfen lassen sich die Verzerrungen in Polnähe (zuungunsten des bisher verzerrungsfreien Äquators mildern), wenn man an Stelle des längentreuen Äquators 2 längentreue Parallelkreise wählt:
Hier ein Entwurf, bei dem die Breite 40° (Nord und Süd) längentreu ist. [Wagner: Entwurf 7]
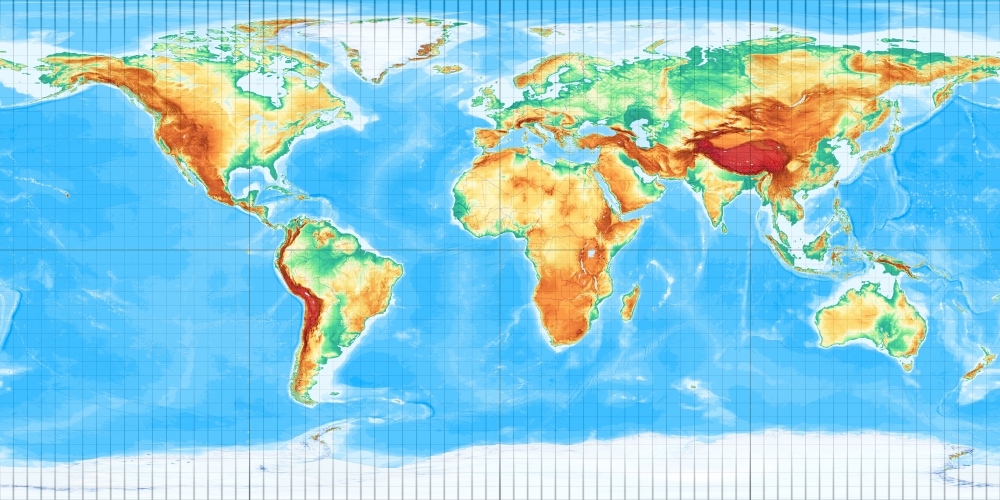
Was ist nun mit dem winkeltreuen Zylinder? Der winkeltreue Zylinderentwurf in polständiger Lage ist ein Klassiker: Die Mercatorprojektion ...
Weil einzig auf der Mercatorkarte ein Schiff mit konstantem Kurs eine Gerade entlangfährt, ist dies der Entwurf fast aller Seekarten, die es gibt.
Die Mercatorkarte ist theoretisch unendlich „hoch“. Je mehr man nach Norden und Süden kommt, desto mehr nähert man sich dem Pol an, ohne diesen allerdings jemals zu erreichen.
Die klassische Schulmeisterkritik an Old Mercator lautet: Grönland ist ja so groß wie Afrika. Dafür stimmen aber die Formen.
Mercator hat den Entwurf 1569 veröffentlicht und wenn er seinen Namen nicht zu Mercator lateinisiert, sondern es beim deutschen Gerhard Kremer gelassen hätte, hieße heute das UTM-Meldegitter der Natokarten nicht UTM-Gitter, sondern UTK-Gitter. [Wagner: Entwurf 10]
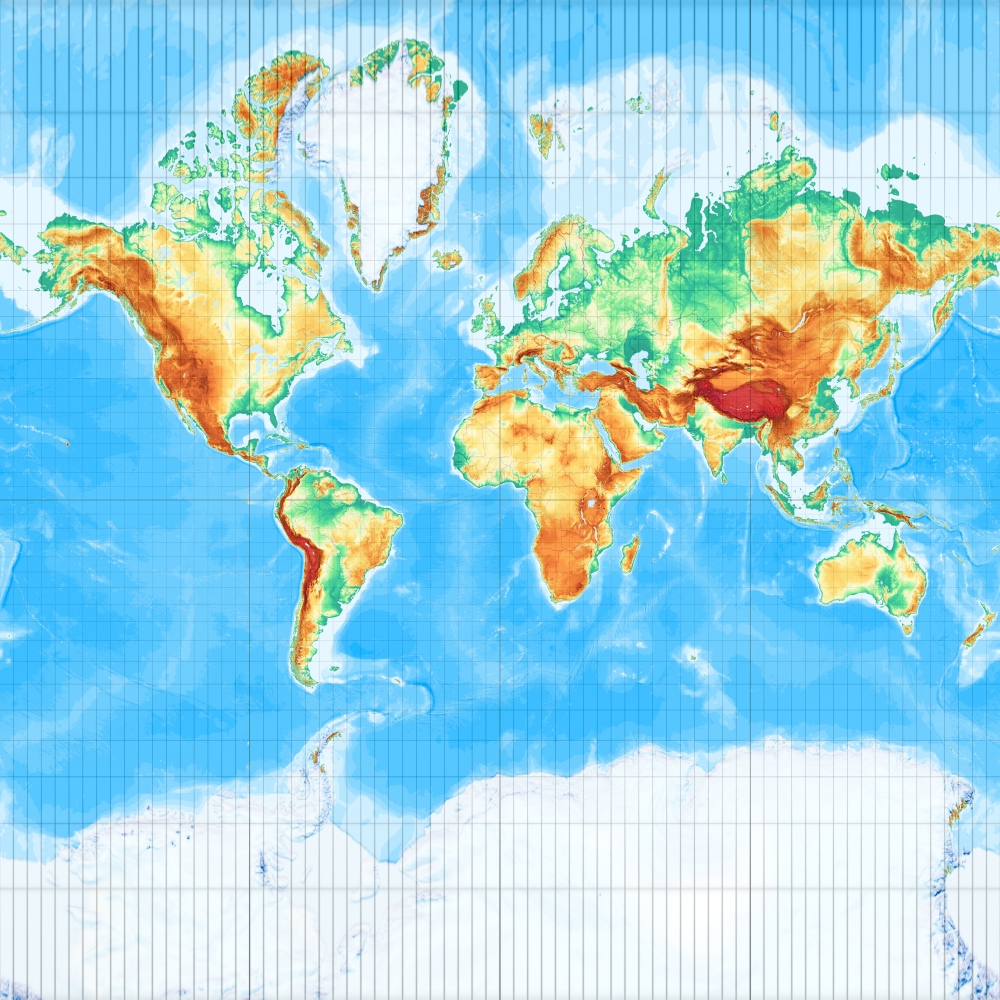
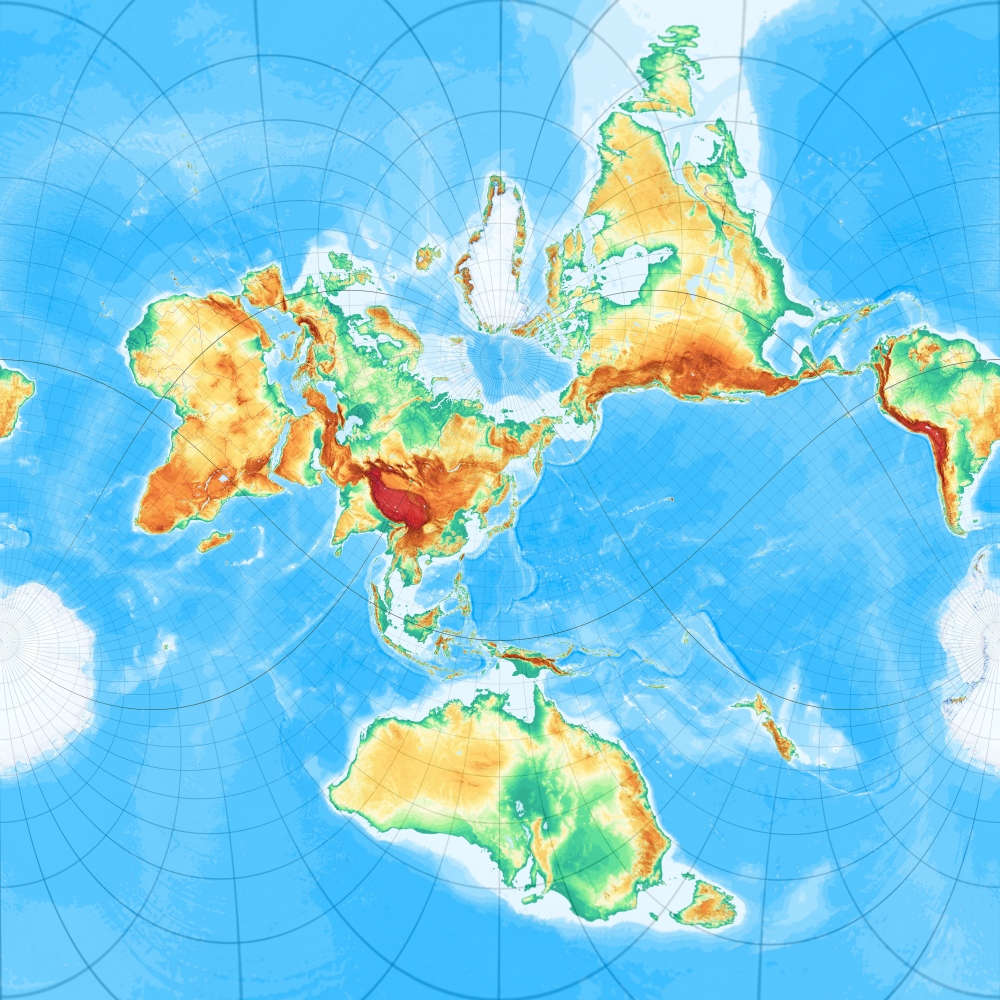
UTM heißt Universal Transversal Mercator. Transversal heißt Drehung der Zylinderachse um 90°. Ansonsten bleibt es beim Mercator. 2 (vom Ansatz her identische) Versionen sind implementiert:
Variante I mit Inversprogramm Zylinder in freier Lage gerechnet
Variante II mit der direkten Spezialimplementation direct_cyt1_cylinder_transversal_mercator.rta gerechnet. Diese blendet die „Zylinderrückseite“ aus.
Ein ungewohntes Weltbild. Und doch der Netzentwurf von 99.99 % aller Landkarten der Welt.
Man betrachte weniger das Gesamt-Weltbild, als den Nullmeridian, in welchem die Erde den Zylinder berührt. Dieser wird nicht verzerrt. Wenn man unsere Mutter Erde nun nicht auf einen, sondern auf 60 um je 6° leicht verdrehte Zylinder abbildet, und jeweils nur ein kleines Gebiet in Berührungsmeridiannähe nutzt, so erhält man 60 Meridianstreifen. In diesen sind die Verzerrungen nur jeweils gering. (Um zu zeigen, was gemeint ist, ist in der Abbildung blau ein fiktiver „10-Grad-Meridianstreifen“ eingezeichnet.) Man erhält so das Netz, dass die Landesaufnahmen der meisten Länder der Welt für ihre topographischen Landeskartenwerke benutzen und auch UTM, die Abbildung des GPS-Systems WGS84 ist (bis auf einen Faktor von 0,9996) eine waschechte Gauß-Krüger-Projektion.
Gauß-Krüger stimmt nicht ganz. Denn das hier vorgestellte Netz wurde auf der Kugel gerechnet. Der Witz des richtigen Gauß-Krüger besteht darin, dass er nicht auf der Kugel, sondern auf dem Rotationsellipsoid gerechnet wird. Das macht es schön kompliziert. Hierzu gibt es zwei gesonderte Themenseiten zum 100jährigen Jubiläum des Gauß-Krüger 2012. In kleinen Maßstäben ist aber die Unterscheidung zwischen (ellipsoidischem) Gauß-Krüger und (sphärischem) querachsigem winkeltreuen Zylinderentwurf bedeutungslos. Mit unbewaffnetem Auge wird man keinen Unterschied bemerken.
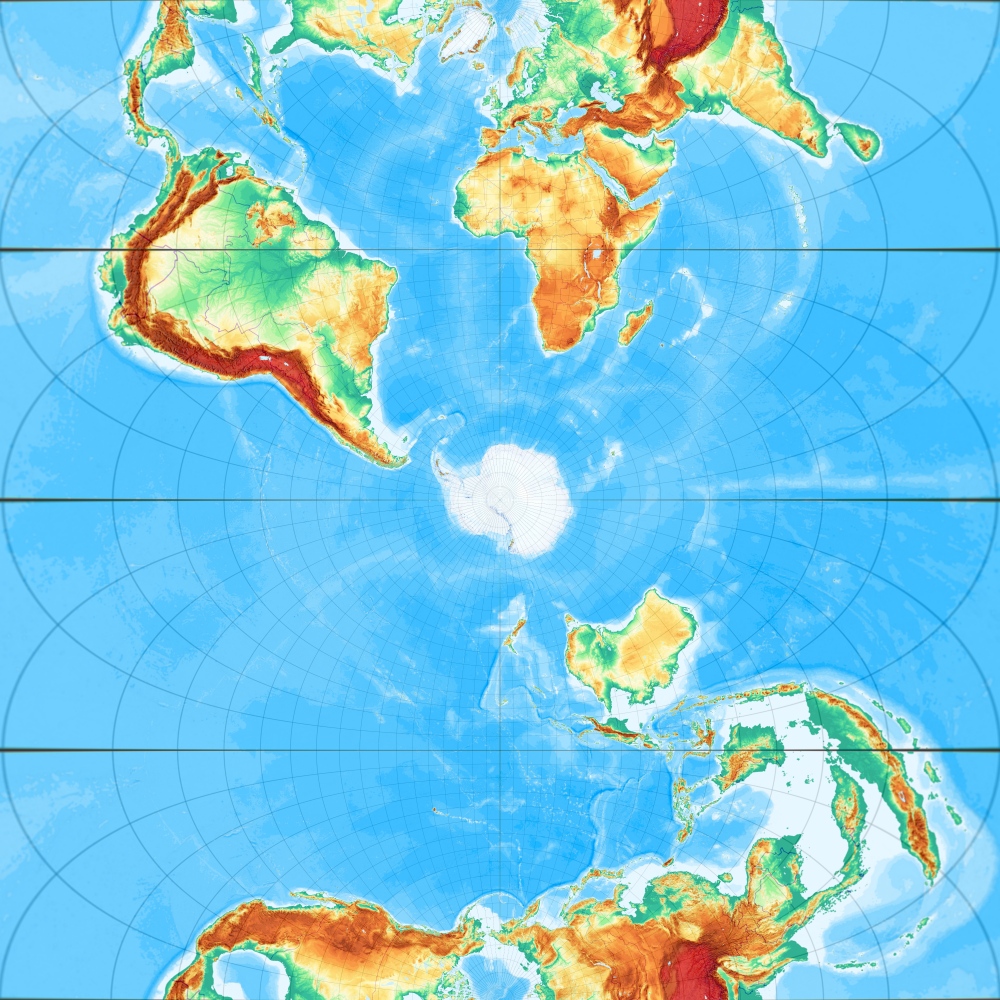
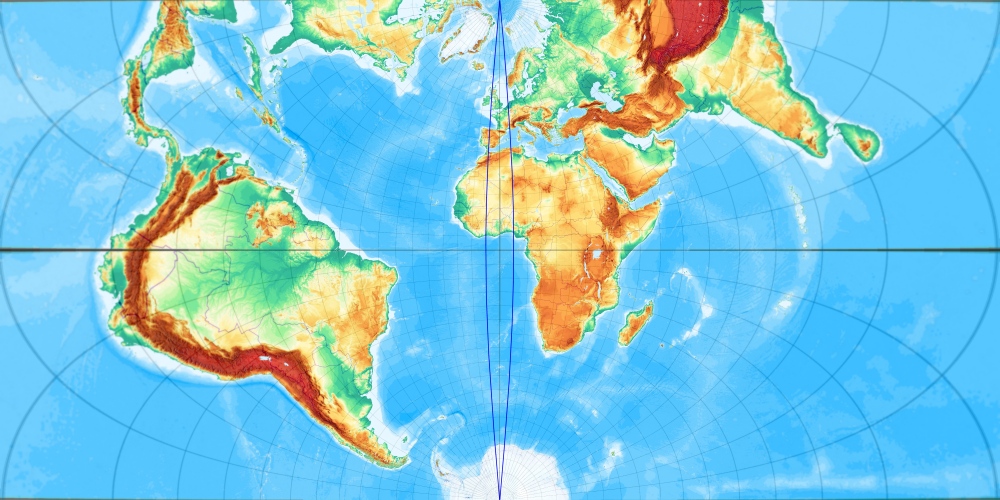
Wenn man die Erde im Zylinder um 90° drehen kann, so kann man sie auch um jeden anderen Winkel drehen. Hier ein mögliches Ergebnis:
Nun ist zur Abwechslung einmal Australien doppelt so groß, wie Afrika. Freie Lagen ergeben ungewöhnliche Weltbilder, aber keinesfalls falsche Weltbilder. Die Welt wird lediglich in einer ungewöhnlich verdrehten Lage betrachtet. Dieser Entwurf winkeltreu und derselbe wie bei der Mercator- oder der Gauß-Krüger-Projektion.
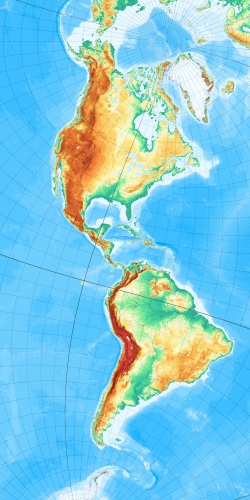
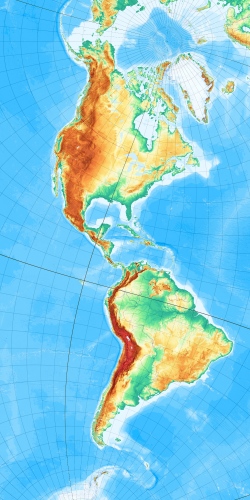
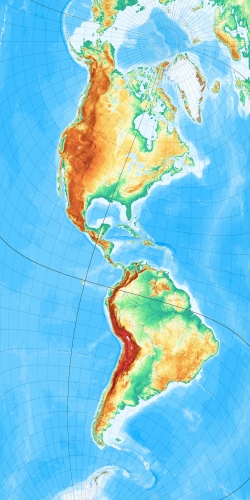
Zylinderentwürfe in freien Lagen lassen sich klassisch dazu einsetzen, langgestreckte Erdoberflächenauusschnitte, exemplarisch Nord- und Südamerika formvollendet abzubilden (siehe z. B. Wagner, S. 141, abb. 75).
Hier drei Beispiele mit einer Erdachsenlage durch den Punkt 15°N/15°O, v. l. n. r
winkeltreu, abstandstreu und flächertreu:
Projektionsanleitung: Prijiziert wird mit „Osten oben“ in ein querliegendes Bild, Breite 2000, Höhe 1000 Pixel. Programme proj_cyf1_cylinder_winkel(abstands/flaechen)treu_frei.rta, man wähle die 4 Parameter scale=100000000, phiP=15, lambdaP=15 und lambda0=-105. Der lambda0-Wert -105° verschiebt lediglich das Kartenbild horizontal, also auf der (um 90° gedrehten) Amerika-Nord-Süd-Achse. Zum Schluss die Karte um 90° drehen, um sie zu norden.
Dies sind längst nicht alle Zylinderentwürfe.
Echte Zylinderentwürfe haben (in polständiger Lage) parallele gerade Meridiane und ebenfalls gerade Parallelkreise. Unterschiedliche Formeln für die Parallelkreisabstände ergeben unterschiedliche Projektionen ...
Andere (echte) Zylinderprojektionen
Wenn man auch gekrümmte oder geknickte Meridiane zulässt, begibt man sich auf das Feld unechter Zylinder. Derartige Entwürfe heissen auch pseudozylindrischen Projektionen ...
Pseudozylindrische (unechte) Projektionen
Assemblerprogramme:
Polare Lagen
Flächentreuer Zylinderentwurf
Flächentreuer Zylinderentwurf mit zwei längentreuen Parallelkreisen
Abstandstreuer Zylinderentwurf (quadratische Plattkarte)
Abstandstreuer Zylinderentwurf mit zwei längentreuen Parallelkreisen (rechteckige Plattkarte)
Winkeltreuer Zylinderentwurf in polständiger Lage (Mercatorprojection)
Winkeltreuer Zylinderentwurf in querachsiger Lage (Direktprogramm)
Freie Lagen
Winkeltreuer Zylinderentwurf in freier Lage
Abstandstreuer Zylinderentwurf in freier Lage
Flächentreuer Zylinderentwurf in freier Lage
18.03.2021 Die alten Müller-Richert-Karten durch W100 ersetzt.