Zum Verzeichnis aller Canters-Netze. Link to Canters Index Table with all projections
[1st subsection: Main projections]
Frank Canters konstituiert seine „Hauptreihe“ ganz akademisch: Die 40 Koeffizienten, die zwei Polynome zweier Veränderlicher bis zum 5. Grad besitzen, werden so gewählt, dass Landflächen der Erde minimal verzerrt werden. Die folgenden Projektionen haben dann immer weniger Koeffizienten.
Low-error polyconic projection obtained through non-constrained optimization

Eine Weltkarte mit einem Weltrekord: Dies ist dasjenige Kartennetz, das die gesamte Landfläche der Erde (ausgenommen die Antaktis) mit den geringsten Streckenverzerrungen abbildet. Weil die Landmasse der Erde ungleich verteilt ist, entsteht ein assymetrisches Kartennetz, übrigens auch mit einer Ost-West-Assymetrie, was man bei genauer Betrachtung bemerkt.
[Canters (2002), p. 190f., Tab. 5.3, Fig. 5.13]
Low-error polyconic projection with straight equator and symmetrry about the central meridian

Wenn man die 40 Koeffizienten des W10 reduziert, wird das Kartenbild allmählich symmetrischer. Hier Canters Netzentwurf mit 16 Koeffizienten, den wir kurz als W11 bezeichnen. Der Äquator ist gerade, die Ungleichheit zwischen Ost und West ist beseitigt, Nord- und Südhalbkugel weisen aber noch verschiedene Linienbilder auf.
[Canters (2002), p. 192f., Tab. 5.4, Fig. 5.14]
Low-error polyconic projection with twofold symmetry
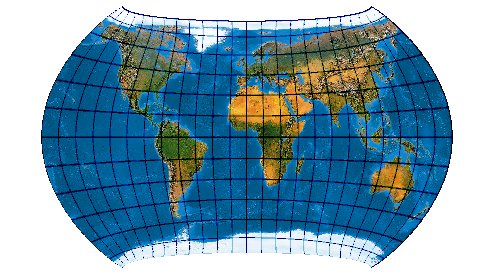
Mit dem W12 erreichen wir allmählich gewohnte Kartenbilder.
[Canters (2002), p. 194f., Tab. 5.5, Fig. 5.15]
Low-error polyconic projection with twofold symmetry and equally spaced equator
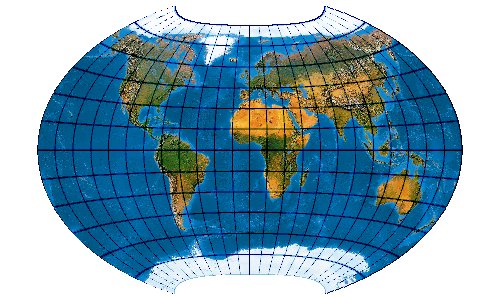
Noch 2 Koeffizienten weniger ... noch ist das Verhältnis von Äquator und Mittelmeridian nicht ganz 2 : 1 ... diese Aufgabe wird der nächste Netzentwurf lösen.
[Canters (2002), p. 196f., Tab. 5.6, Fig. 5.16]
Low-error polyconic projection with twofold symmetry, equally spaced parallels and a correct ratio of the axes.
Der klassische Canters
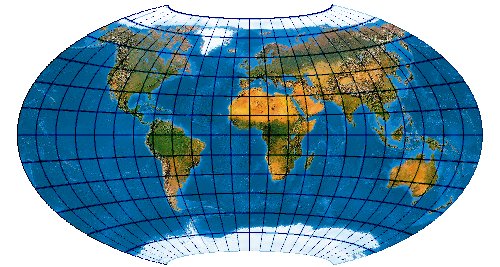
Dieses Netz bewertet der Netzentwurfs-Kritiker mit: „Gib mir Worte zu schwärmen“ *
Der klassische Canters W14 im Großbildmaßstab 1:200.000.000 (etwa 500 kByte)
Ein Netz nicht nur mit sehr geringen Verzerrungen, sondern auch von wunderbarer Eleganz. Weil der W14 auch der bekannteste Low-error von Canters ist, er oft auch als Canters Low error polyconic schlechthin bezeichnet.
[Canters (2002), p. 198f., Tab. 5.7, Fig. 5.17]
[2nd subsection: Pseudocylindric Projections]
Immer dann, wenn zonale Erscheinungen, wie z. B. Klima- oder Vegetationszonen abzubilden sind, sollten die Breitenkreise nicht gekrümmt, sondern gerade sein. Canters stellt 4 derartige Netze mit jeweils optimierten Verzerrungen vor. Vgl. hierzu auch die Seite Pseudozylindrische Netze
Low-error pseudocylindrical projection with twofold symmetry

[Canters (2002), p. 200f., Tab. 5.8, Fig. 5.18, Evenden (2005) 5.2.44]
Low-error pseudocylindrical projection with twofold symmetry and a pole line half the langth of the equator
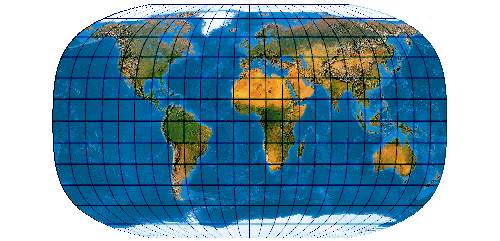
Pollinie in halber Äquatorlänge
[Canters (2002) p. 200ff., Tab. 5.9, Fig. 5.19, Evenden (2005) 5.2.44]
Low-error pseudocylindrical projection with twofold symmetry and a correct ratio of the axes

Korrekte Verhältnis Äquator zu Mittelmeridian.
[Canters (2002) p. 203f., Tab. 5.10, Fig. 5.20, Evenden (2005) 5.2.44]
Low-error pointed-polar pseudocylindrical projection with twofold symmetry and a correct ration of the axes
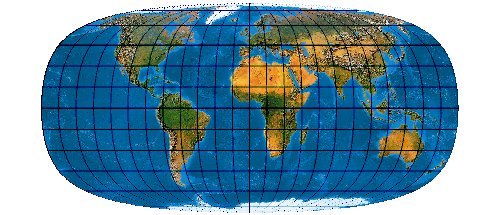
Die Formel enthält einen Koeffizienten 0.3385, der sich mitunter als -0.3385 implementiert findet und dann folgendes Bild erzeugt. — There is a 0.3385 coefficient in the original formula but Evendens graticule is given with -0.3385:
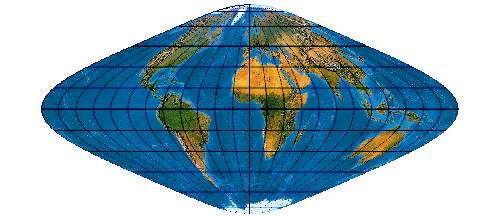
[Canters (2002) p. 203f., Tab. 5.10, Fig. 5.20, Evenden (2005) 5.2.44]
[3rd subsection: Polyconicals with Pole as Point]
Während die bisherigen Projektionen (außer dem Canters W19) Pollinien aufwiesen, soll nun ein Netz mit dem Pol als Punkt entwickelt werden. Ein Pseudozylinder (wie der Canters W19) würde mit seinen geraden Parallelkreisen eine starke Schiefschnittigkeit in höheren Breiten bewirken. Aus diesem Grund baut Canters hier auf einem van der Grinten-Entwurf auf ...
Low-error pointed-polar polyconic projection with twofold symmetry equally spaced parallels a correct ration of the axes
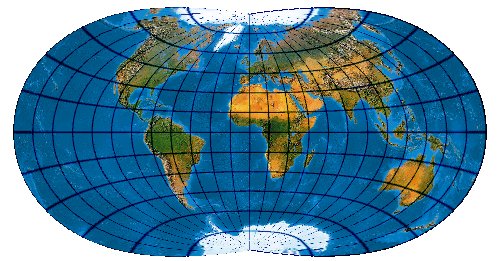
[Canters (2002) p. 205f., Tab. 5.11, Fig. 5.2]
[4th subsection: Oblique Projections]
Eine andere Möglichkeit, Verzerrungen der Kontinente zu mildern besteht darin, schiefe Erdlagen zu nutzen. Hierbei wird die Erde in sich selbst so verdreht, dass die Landmasse in Kartengebieten mit geringeren Verzerrungen abgebildet wird.
Low-error simple oblique polyconic projection with pointed meta-pole and constand scale along the axes.
Hier zunächst das Netz in normaler Lage. Normal aspect:

Nun das Kartenbild mit sphärischer Verdrehung der Erdoberfläche. Oblique aspect:

Allgemeine Optimierung der Landflächen ohne Antarktis. Weil sich der größte Teil der Landmasse auf der Nordhalbkugel befindet, ist der Süden weniger optimal abgebildet, was letztendlich zu der Spaltung Südafrikas führt.
[Canters (2002) p. 209f., Tab. 5.13, Fig. 5.24]
Low-error simple oblique polyconic projection with pointed meta-pole and constand scale along the axes, centered at 45°N, 20°E.
Die geteilte Afrika-Spitze wird vermieden, indem man den Nordpol etwas weiter oben anordnet und erneut optimiert.
Hier wieder das Netz zunächst in normaler Lage:

Nun das entgültige Kartenbild mit der sphärischen Verdrehung der Erdoberfläche:

[Canters (2002) p. 211f., Tab. 5.14, Fig. 5.25]
Low-error plagal aspect polyconic projection with pointed meta-pole (30°N, 140°W), geographical North Pole at meta-longitude of 30°, and constant scale along the axes.
Schließlich soll auch Antarktika in die Optimierung einbezogen werden. Dies gelingt nur, wenn der Nordpol aus der Zentrallage in eine sog. plagale Lage transsformiert wird.
Normale Lage:

Entgültige, schiefe („plagale“) Lage. Die Antarktis ist nicht mehr geteilt:
Der plagale Canters

Der plagale Canters C8-6 als Großbild 1:200.000.000 (etwa 500 kByte)
[Canters (2002) p. 209f., Tab. 5.13, Fig. 5.24]
Frank Canters ist offenbar auch ein großer Verehrer der Weltkartennetze von Karlheinz Wagner. Wagner, der seine Netze um 1940 (übrigens als Lehrmeister von Werner Stams und Günther Mokronowski [die wiederum meine Lehrer waren]) mühsam mit Rechenschieber und Logarithmentafel gerechnet hat, wird nun von Canters hinsichtlich der Verzerrungen optimiert.
Optimised version of Wagner I (Canters W01)
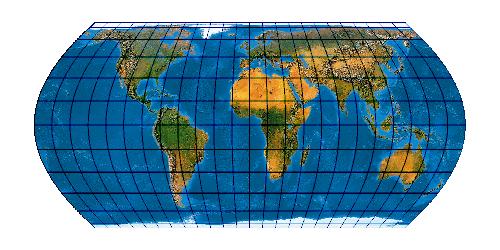
[Canters (2002), p. 180ff., Tab. 5.1, Fig. 5.5, 5.7]
Optimised version of Wagner II (Canters W02)
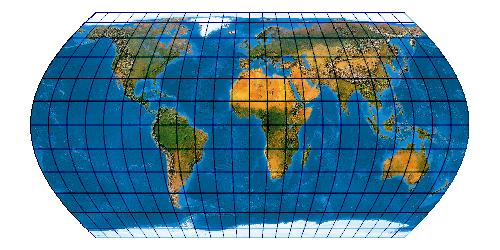
[Canters (2002), p. 180ff., Tab. 5.1, Fig. 5.5, 5.8]
Optimised version of Wagner VI (Canters W06)
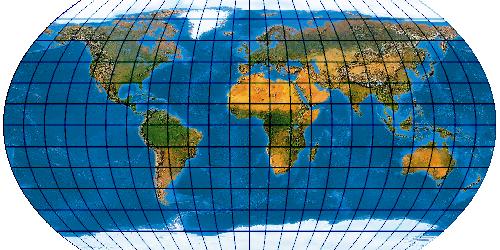
[Canters (2002), p. 184ff., Tab. 5.1, Fig. 5.5, 5.6]
Batwing map. Optimised version of Wagner VII (Hammer-Wagner-Canters or Canters W07)
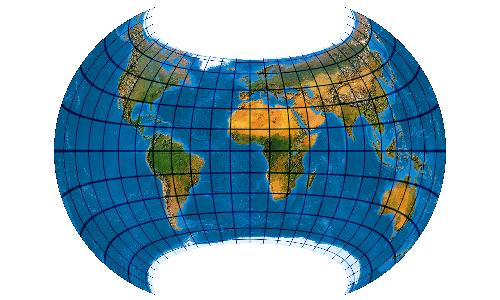
[Canters (2002), p. 184ff., Tab. 5.2, Fig. 5.9, 5.11]
Vgl. hierzu auch den von mir verfassen Aufsatz „Variationen von Weltkartennetzen der Wagner-Hammer-Aïtoff-Entwurfsgruppe“ in den Kartographischen Nachrichten Nr. 1/2006.
Hier die Karte als Großformat (800 kByte) im Maßstab 1:200.000.000 (bei 254 dpi).
Optimised version of Wagner VIII (Canters W08)
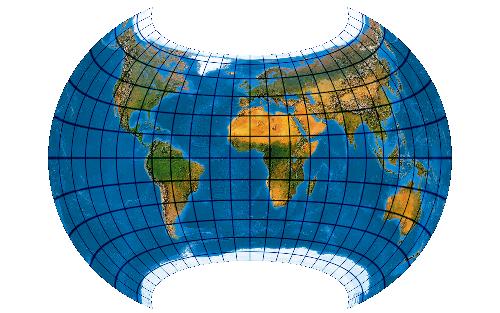
[Canters (2002), p. 184ff., Tab. 5.2, Fig. 5.9, 5.12]
Hier die Karte als Großformat (800 kByte) im Maßstab 1:200.000.000 (bei 254 dpi).
Optimised version of Wagner IX (Aitoff-Wagner-Canters or Canters W09))
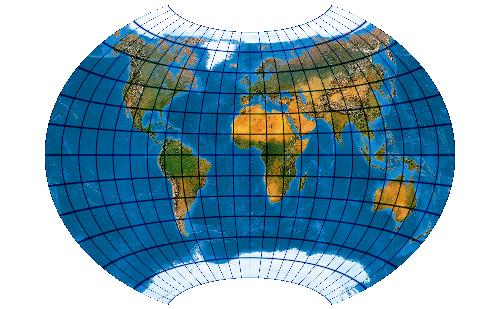
[Canters (2002), p. 184ff., Tab. 5.2, Fig. 5.9, 5.10]
Ein weiteres Verfahren Canters' besteht darin, bekannte Netze („Mutterentwürfe“) nachzubearbeiten, um deren Verzerrungen zu mildern. Diese Behandlung erfolgt so, dass dabei die Flächentreue der Mutterentwürfe gewahrt bleibt.
Es erfolgt keine Projektion Erde in Kartenebene, sondern eine Abbildung der Kartenebene eines Mutterentwurfes (Wagner VII, Hammer, Mercator-Sanson) in eine Ziel-Kartenebene.
Infolge des doppelten Resamplings haben diese Verfahren allerdings den Mangel einer leichten numerischen Instabilität.
Low-error equal-area transformation of Hammer-Wagner [Wagner VII] with twofold symmetry and a correct ratio of the axes
Post-Transformation des Wagner VII.
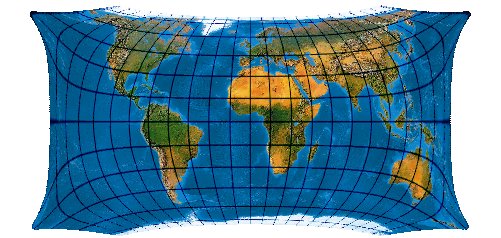
[Canters (2002) p. 215f., Tab. 5.16, Fig. 5.27]
Low-error equal-area transformation of Hammer-Wagner [Wagner VII] with twofold symmetry and constant scale along the equator
Post-Transformation des Wagner VII, andere Variante.
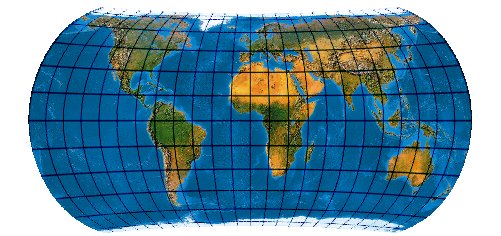
Genau genommen hat der C6 No. 6 (W31) nur noch drei Koeffizienten, so dass er eigentlich exakt als C3 No. 3 bezeichnet werden müsste; aus methodischen Gründen wird er aber in der C6-Reihe belassen. Dies gilt auch für die folgenden Post-Transformationen C6 No. 7, No 8. und No. 9 (W32, W33, W34)
[Canters (2002) p. 216., Tab. 5.17, Fig. 5.28]
Low-error equal-area transformation of Hammer-Aïtoff with twofold symmetry and a constant scale along the equator
Post-Transformation des Hammerschen (alias Hammer-Aïtoffschen) Entwurfes. Die Flächentreue bleibt gewahrt.
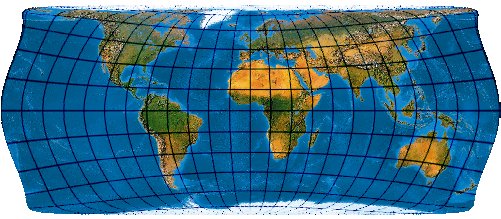
[Canters (2002) p. 217., Tab. 5.18, Fig. 5.29]
Low-error equal-area transformation of the sinusoidal projection [Mercator-Sanson] with twofold symmetry, equally divided, straight parallels and a correct ratio of the axes (not including Antarctica in the optimisation)
Interessant, was Canters Optimierung mit dem eigentlich etwas antiquiert geltenden Mercator-Sanson anstellen kann. Das Ergebnis erinnert auch an Max Eckert-Greiffendorfs Netze.
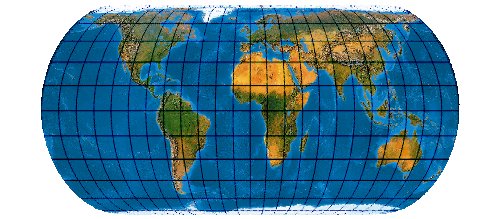
[Canters (2002) p. 218f., Tab. 5.19, Fig. 5.30]
Low-error equal-area transformation of the sinusoidal projection [Mercator-Sanson] with twofold symmetry, equally divided, straight parallels and a correct ratio of the axes (including Antarctica in the optimisation)
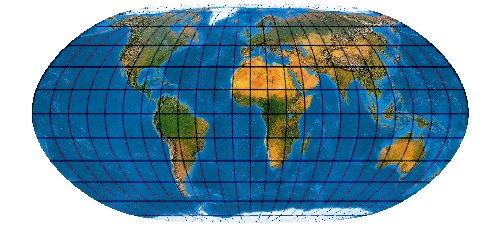
Wie C6-8, allerdings unter Einschluss der Antarktis in die Optimierung.
[Canters (2002) p. 219f., Tab. 5.20, Fig. 5.31]
Assemblerprogramme mit denen die Netzentwürfe gerechnet wurden:
Canters Low-error Projection W10 (Direkttransformationprogramm)
Canters Low-error Projection W11 (Direkttransformationprogramm)
Canters Low-error Projection W12 (Direkttransformationprogramm)
Canters Low-error Projection W13 (Direkttransformationprogramm)
Canters Low-error Projection W14 (Direkttransformationprogramm)
Canters Low-error Projection W15 (Pseudozylinder I) (Direkttransformationprogramm)
Canters Low-error Projection W16 (Pseudozylinder II) (Direkttransformationprogramm)
Canters Low-error Projection W17 (Pseudozylinder III) (Direkttransformationprogramm)
Canters Low-error Projection W19 (Pseudozylinder IV) (Direkttransformationprogramm)
Canters Low-error Projection W19 (Pseudocylinder IV/Rhombic shape of G. I. Evenden) (Direkttransformationprogramm)
Canters Low-error Projection W18 (Direkttransformationprogramm)
Canters Low-error Projection W20 (schiefachsig) (Direkttransformationprogramm)
Canters Low-error Projection W21 (schiefachsig) (Direkttransformationprogramm)
Canters Low-error Projection W23 (schiefachsig) (Direkttransformationprogramm)
Canters Wagner I-Optimierung W01 (Direkttransformationsprogramm)
Canters Wagner II-Optimierung W02 (Direkttransformationsprogramm)
Canters Wagner VI-Optimierung W06 (Direkttransformationsprogramm)
Canters Wagner VII-Optimierung W07 (Direkttransformationsprogramm)
Canters Wagner VIII-Optimierung W08 (Direkttransformationsprogramm)
Canters Wagner IX-Optimierung W09 (Direkttransformationsprogramm)
Canters Low-error Projection W30 (Direkttransformationprogramm/Post-Transformation nach Wagner VII)
Canters Low-error Projection W31 (Direkttransformationprogramm/Post-Transformation nach Wagner VII)
Canters Low-error Projection W32 (Direkttransformationprogramm/Post-Transformation nach Hammer)
Canters Low-error Projection W33 (Direkttransformationprogramm/Post-Transformation nach Mercator-Sanson)
Canters Low-error Projection W34 (Direkttransformationprogramm/Post-Transformation nach Mercator-Sanson)
Für die Netze C8-4, C8-5, C8-6, braucht man etwas Erfahrung. Es werden benötigt:
Sphärische Metaabbildung der Erdkugel auf sich selbst
Man wähle die Programmparameter der sphärischen Metaabbildung phiP, lambdaP, lambda0 wie folgt:
- C8-4: -29, -24, 180
- C8-5: -45, 20, 180
- C8-6: -30, 40, 150
Die Entwürfe C6-5, C6-6, C6-7, C6-8 und C6-9 sind ebenfalls nicht ganz leicht herstellbar. Es müssen zuvor die Projektionen Wagner VII, Hammer bzw. Mercator-Sanson gerechnet werden.
* Zitat aus dem Deutschlandfunk.