Die größte Herausforderung beim Entwerfen von Kartennetzen ist die formvollendete Konstruktion von Abbildungen der gesamten Erde.
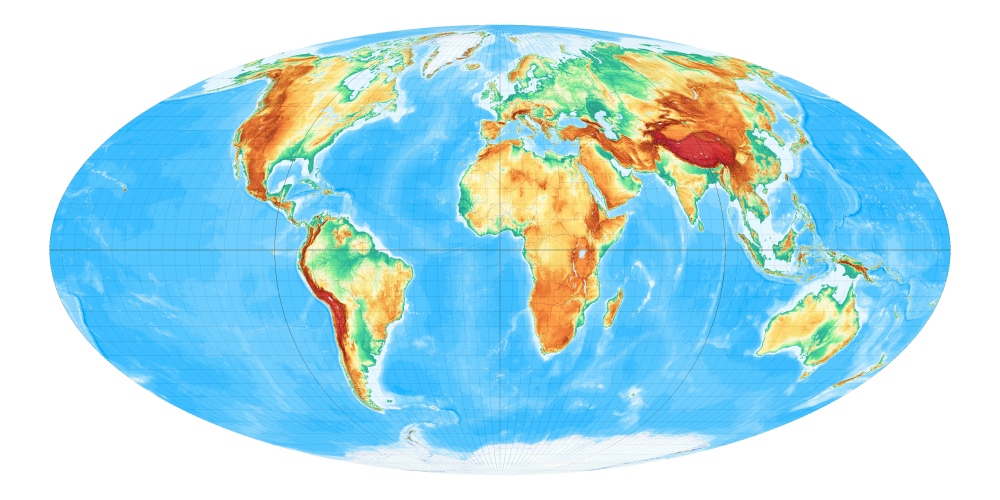
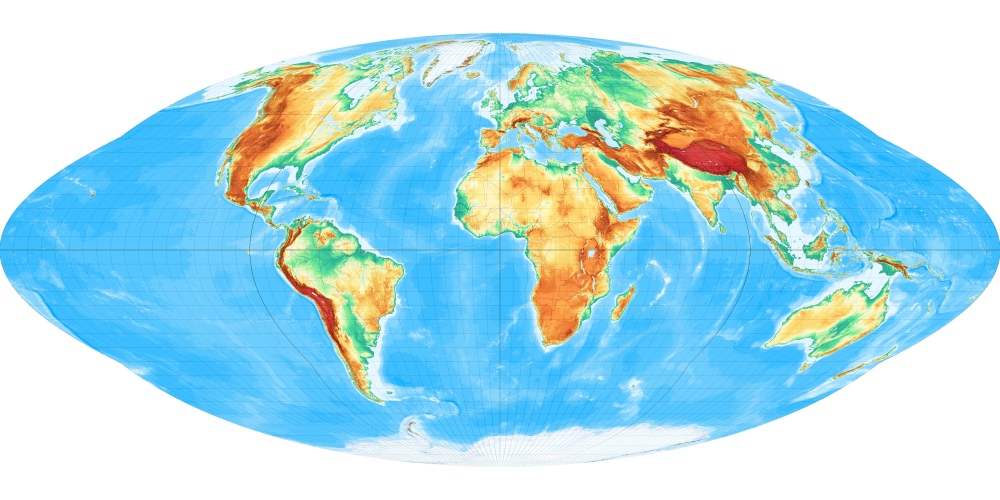
1805 wurde von Karl Mollweide ein Netz publiziert, welches seit 1857, nachdem es der Franzose Jaques Babinet empfohlen hat, weite Verbreitung fand:
Das Mollweidesche Netz ist flächentreu und hat damit eine von Geographen immer wieder hoch bewertete Grundeigenschaft. Man kann es vom Netz des Apianus daran unterscheiden, dass die Parallelkreise nicht mehr gleichabständig sind. [Entwurf 17a bei Wagner]
Hier die Karte als Großformat (800 kByte) im Maßstab 1:200.000.000 (bei 254 dpi).
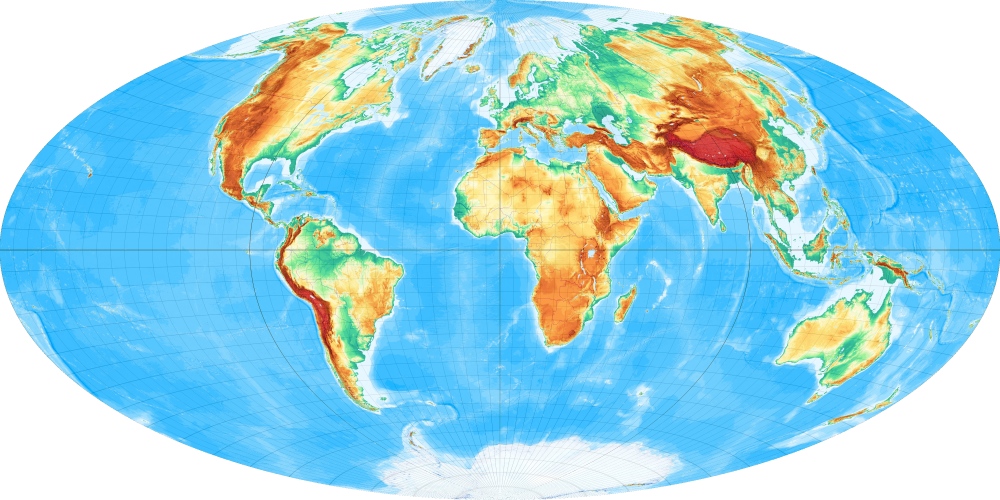
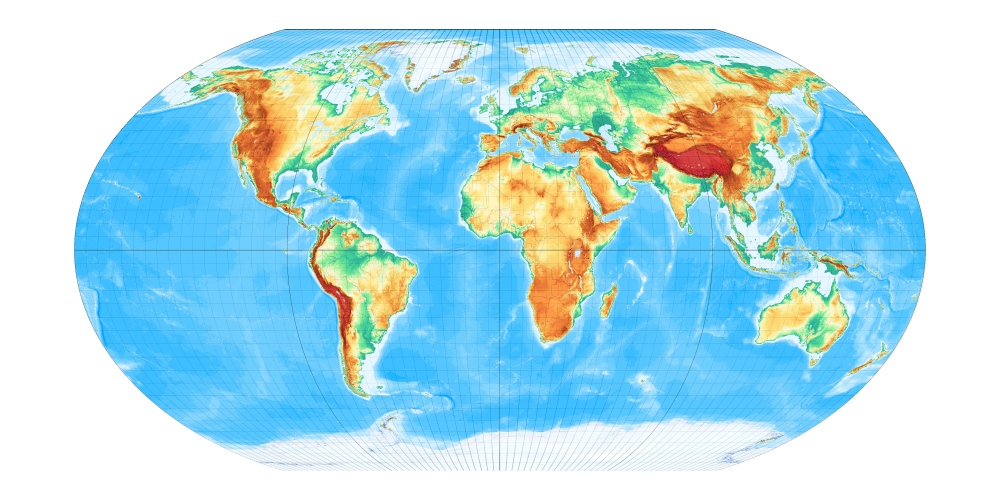
1884 hatte der russische Geograph Aïtoff eine Idee, die viele Weltkarten bis zum heutigen Tag maßgeblich prägen: Er erzeugte aus dem querachsigen abstandstreuen Azimutalentwurf ein Weltkartennetz, indem er dessen inneren verzerrungsärmeren Bereich auf die ganze Erde ausdehnte.
Die Parallelkreise krümmen sich, so lassen sich Aussenbereiche viel verzerrungsärmer als mit dem Mollweideschen Entwurf abbilden. [Entwurf 21a bei Wagner]
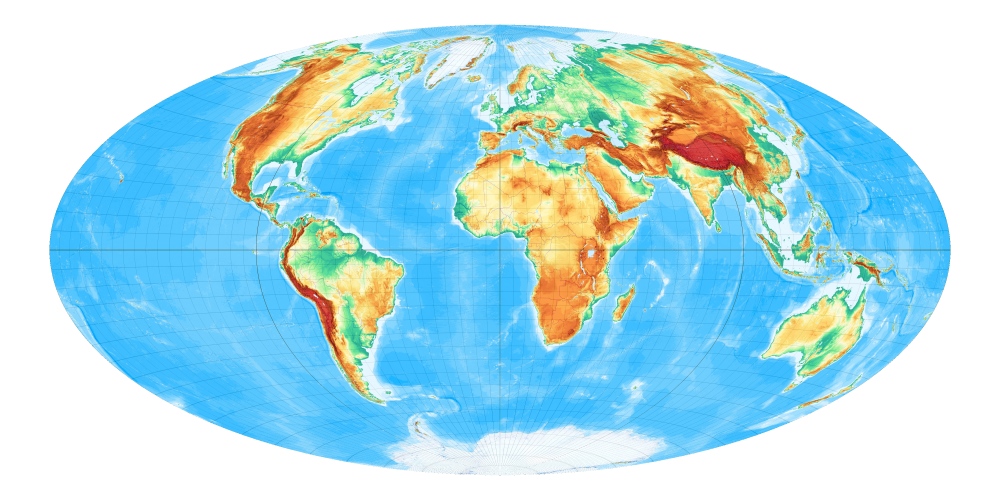
Im Jahr 1892 betrachtete der Geodät Ernst Hammer den Aïtoffschen Entwurf in Petermanns Mitteilungen und tauschte dabei den querachsigen abstandstreuen Azimutalentwurf gegen sein flächentreues Pendant:
Das gefällige Aussehen, sowie die geschätzte Flächentreue hat diesem Entwurf eine schnelle und weite Verbreitung gesichert. In ihm sind seit dem viele Weltkarten entworfen worden. [Entwurf 20a bei Wagner]
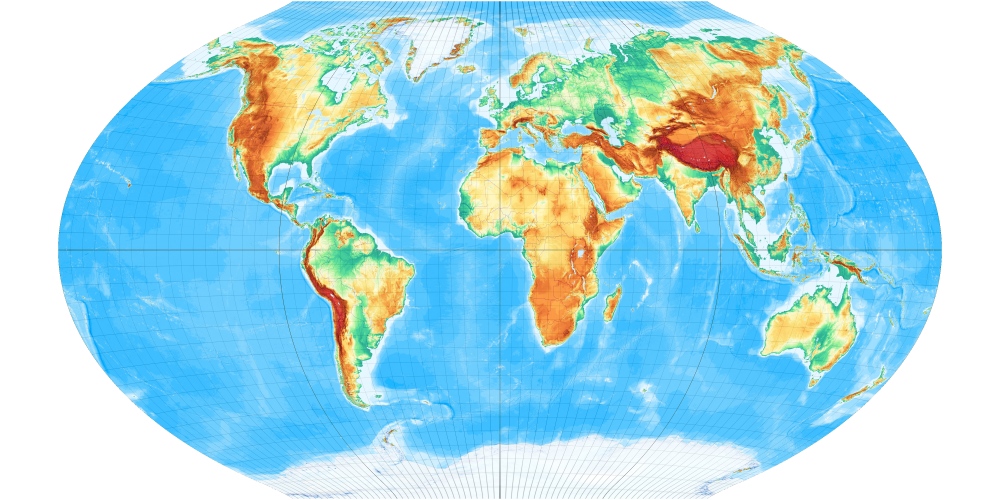
Der Winkelsche Entwurf aus dem Dezemberheft von PGM 1921 (oft falsch zitiert als 1913) ist ein Klassiker, der bis heute sehr viele Weltkarten von Haacks Großem Weltatlas bis The Times Atlas of the World prägt. Auch die National Geographic Society nutzt ihn seit einigen Jahren wieder verstärkt an Stelle der vorher benutzten Robinson-Projektion. Um genau zu sein, „Winkels Tripel“, denn seine Veröffentlichung stellt noch 2 weitere Entwürfe vor, die sich aber nicht durchgesetzt haben:
Winkelscher Entwurf als Großformat (199 kByte)
im Maßstab 1:200.000.000 (bei Auflösung 254 dpi)
Winkel schuf mit der Pollinie (Nord- und Südpol sind jeweils Linien von halber Äquatorlänge) ein völlig neuartiges Weltkartenbild. Hier die Beschreibung des Entwurfs im „Wagner“:

Das Problem des Winkelschen Entwurfs ist, dass er sich nicht invertieren lässt, d. h. dass sich seine Formel aus Form x,y = f(λ,φ) nicht in einfacher Art in die inverse Form λ,φ=g(x,y) umstellen lässt.
Ich habe etwa 4 Jahre daran geknobelt. Der Cengizhan Ipbüker, I. Öztug Bildirici 2002 war mir eine Nummer zu hoch. Evenden lieferte in seinem neuen Libproj.4 Manual von 2008 einen zu verstehenden Text. Aber erst Jakob Brunner aus der Schweiz hat mir 2010 auf die entscheidenden Sprünge geholfen. Meinen eigenen Implementationsreihen der sog. Evenden-Brunner-Iteration hier eine eigene Seite, mit freundlichen Grüßen an Jakob Brunner, Luzern und Friedrich Krumm, Stuttgart.
Hier der Link auf die die wertvolle Originalveröffentlichung, sowie die von Markus Scherer, Karlsruhe besorgte Übersetzung: Winkler, O.: Neue Gradnetzkombinationen. Gotha: Perthes, Petermanns Geographische Nachrichten (Dezember) 1921. Band 67, S. 248-252. Ich bedanke mich herzlich bei Tobias Jung für diese Mitteilung.
Oft zitiert und originell gerechnet: Der Goode Homolosine ist ein Mercator-Sanson, dessen Spitzpoligkeit dadurch beseitigt wurde, dass oberhalb von 40,73° ein Mollweide passend angesetzt wird.
Der olle Goode hat den Trennparallel zwar so gewählt, dass die Meridiane nicht springen, einen kleinen Knick hat er aber doch nicht ganz verhindern können. Das nervt den auf Stetigkeit der Ableitungen achtenden Differentialgeometer vielleicht mehr, als das Auge des Praktikers.
1953 ist ein weiterer Kartennetzentwurf dem Läufer des Rechenschiebers entsprungen, der es zu einiger Berühmtheit bringen sollte: Robinson-Projektion.
Für dieses Netz gibt es keine Formel, Robinson hat vielmehr nur Stützstellen alle 5 Grad angegeben. Man muss zum Berechnen also in einer Tabelle interpolieren.
Weil es nun verschiedene Möglichkeiten der Interpolation gibt, heisst dies, dass die Robinson-Projektion nicht völlig eindeutig definiert ist.
Eigenartigerweise gibt es aber auf den Homepage von Esque und Bergada aus Barcelona (s. RTA-Quelltext und Linkverzeichnis auf der Hauptseite) doch eine analytische Formel. Gibt es eine heimliche Quelle, oder haben Esque und Bergada ein Interpolationspolynom synthetisiert?
Assemblerprogramme:
Mollweides Kartennetzentwurf
Der Aïtoffsche Entwurf
Der Hammersche Entwurf
Der Winkelsche Entwurf (Normale Inversrechnung, diese ist allerdings recht langsam)
Der Winkelsche Entwurf (Normale Inversrechnung, etwas schneller)
Der Winkelsche Entwurf (Direktprogramm, Vorzugsvariante)
Der Winkelsche Entwurf, umlaufend (Normale Inversrechnung, diese ist allerdings recht langsam)
Der Winkelsche Entwurf, umlaufend (Normale Inversrechnung, etwas schneller)
Der Winkelsche Entwurf, umlaufend (Direktprogramm)
Der Winkelsche Entwurf, Brunners Formel (Direktprogramm, sog. Brunnercode, der in den Inmversprogammen gerechnet wird)
Goode Homolosine (Direktprogramm)
Robinson-Projektion, tabellierende Originalversion
Robinson-Projektion, polynomische Variante nach Esque und Bergada
17.03.2021 W100