[Abbildung: Wagner S. 33]

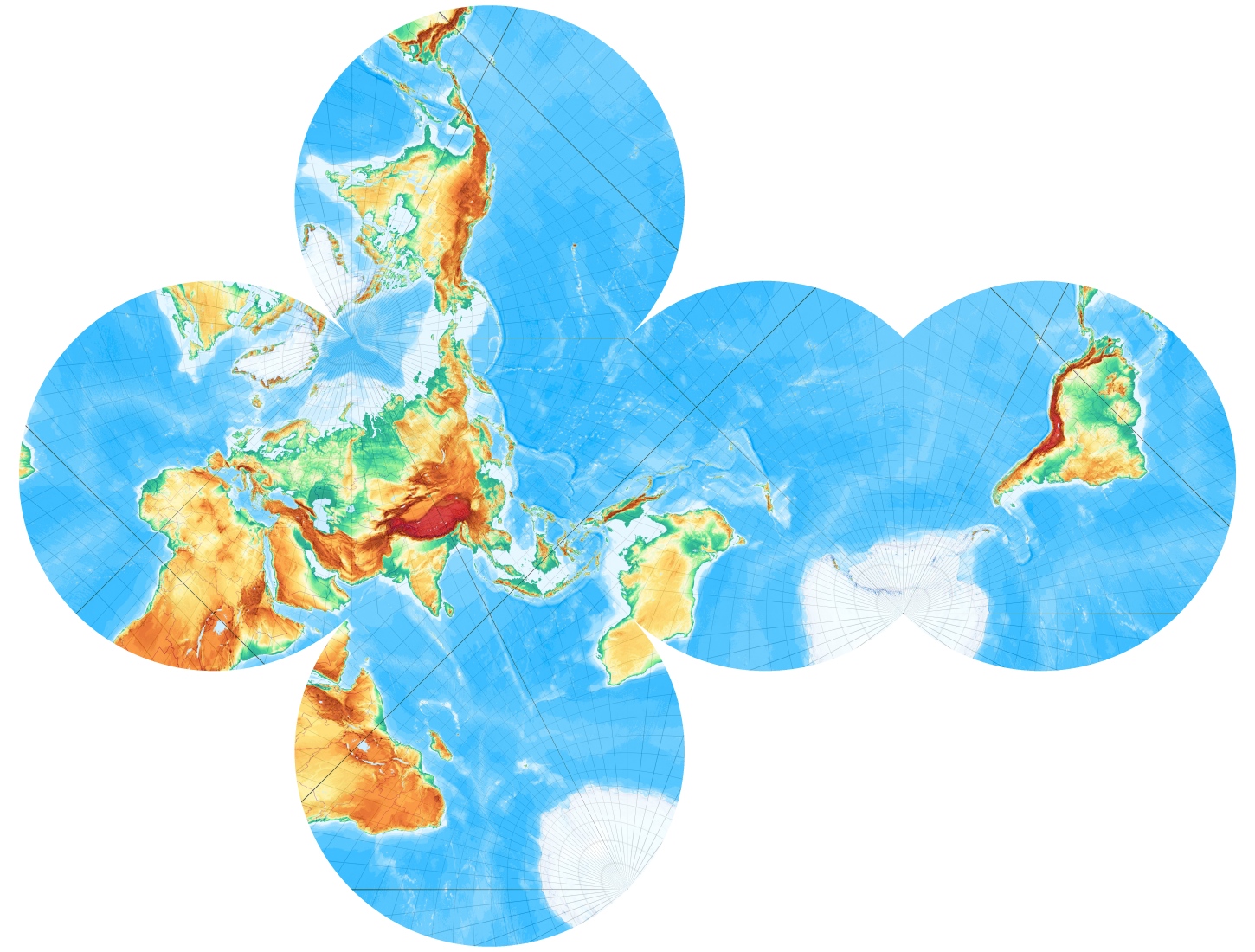
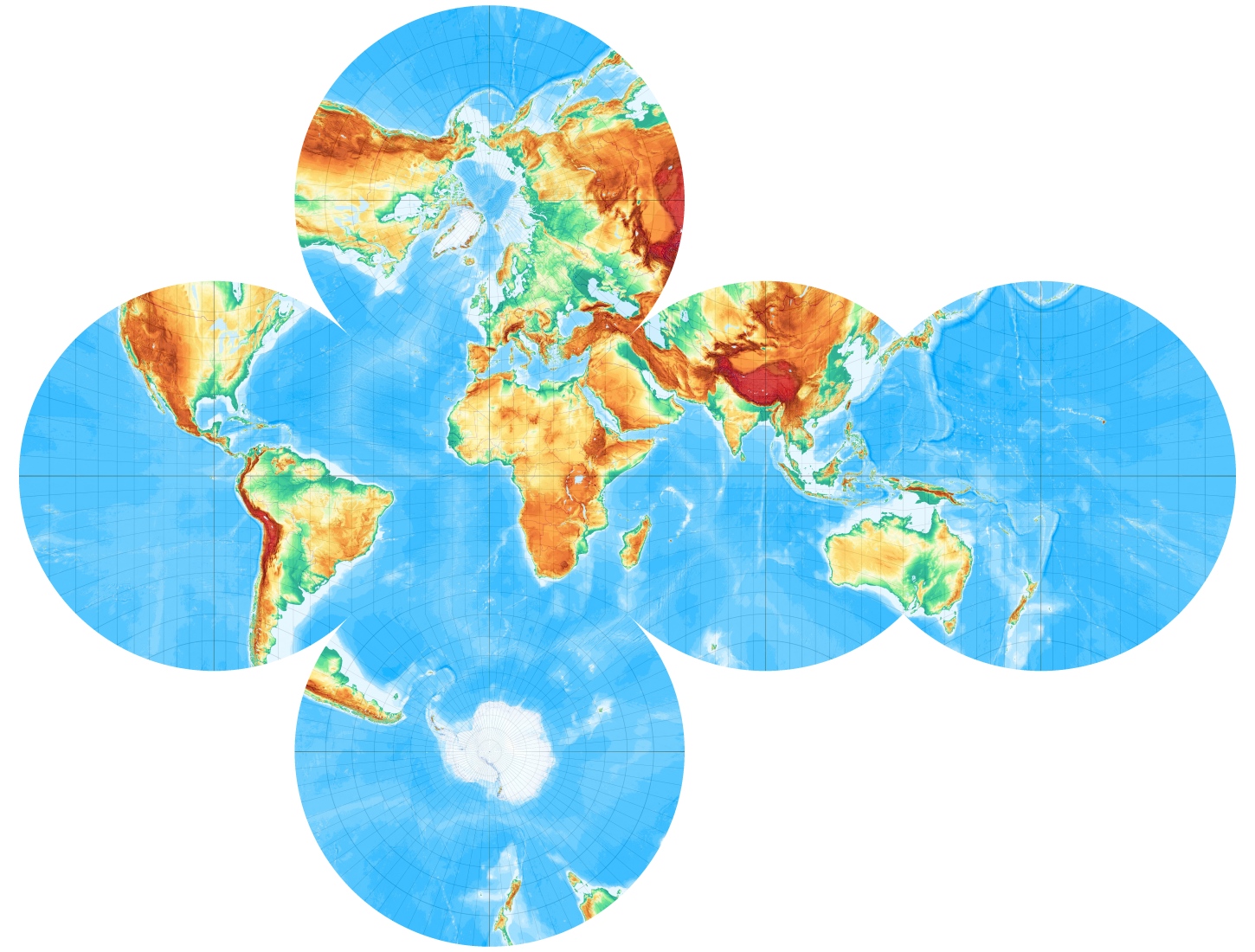
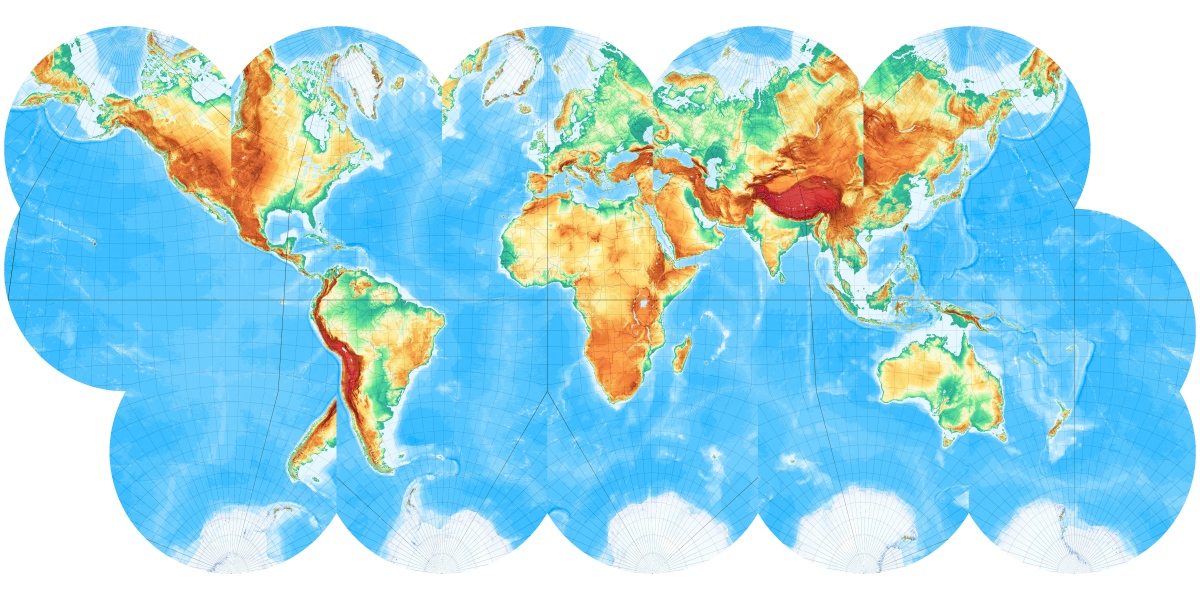
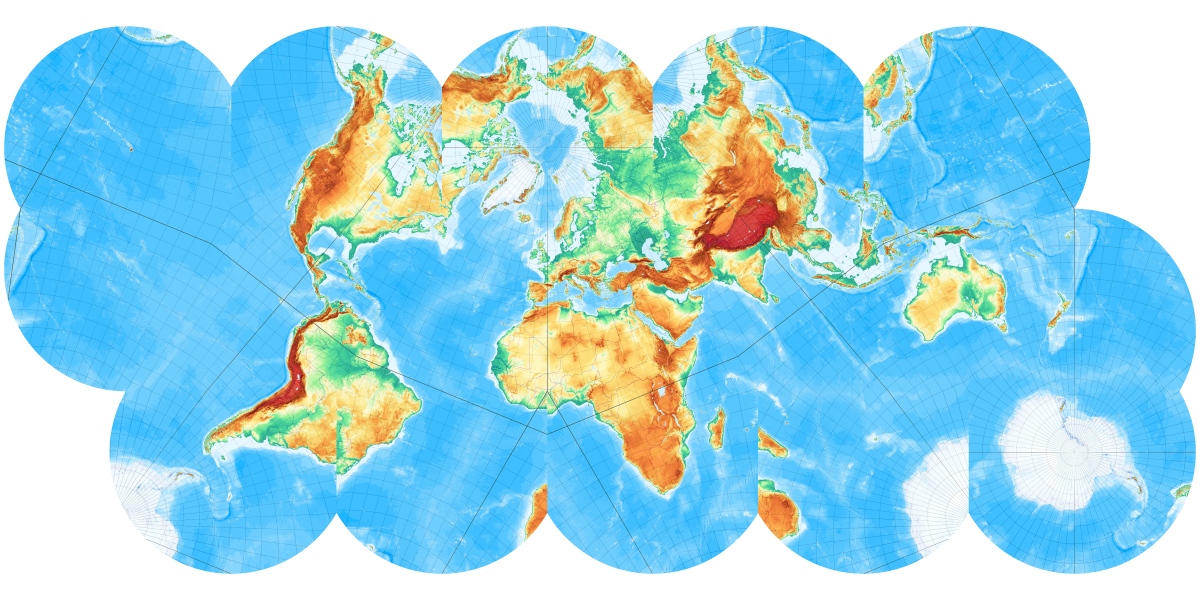
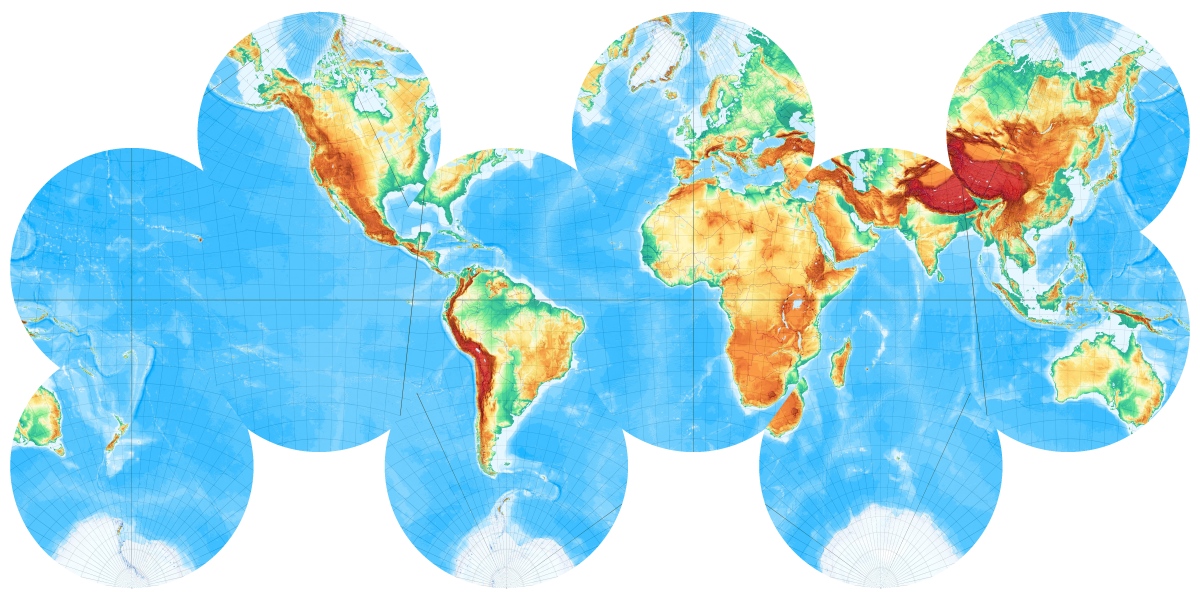
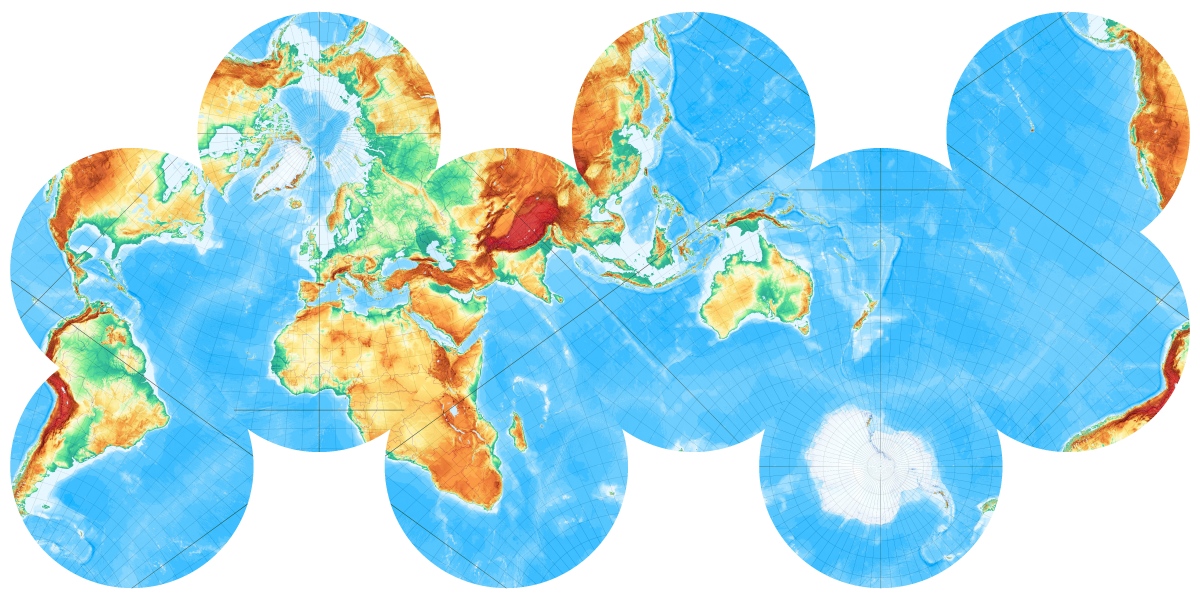
Was passiert eigentlich, wenn man sich die Erde in einem Würfel vorstellt und die Erdkugel auf die Würfeloberfläche projiziert?

Die Erde im Würfel

Es wurden nicht nur die jeweiligen Quadratflächen projiziert sondern etwas größere Bereiche (die Umkreise der den Würfel begrenzenden Quadrate). Das hat den Vorteil, dass man „den Bastelbogen“ nicht ganz exakt entlang der Würfelkanten „ausschneiden“ und „falzen“ muss. Die jeweiligen Kartenflächen laufen an den Kanten jeweils etwas weiter. So lassen sich kleine Ungenauigkeiten ausgleichen. Die Knick- und Schnittlinien lassen sich am Grandnetz zumeist leicht erkennen.

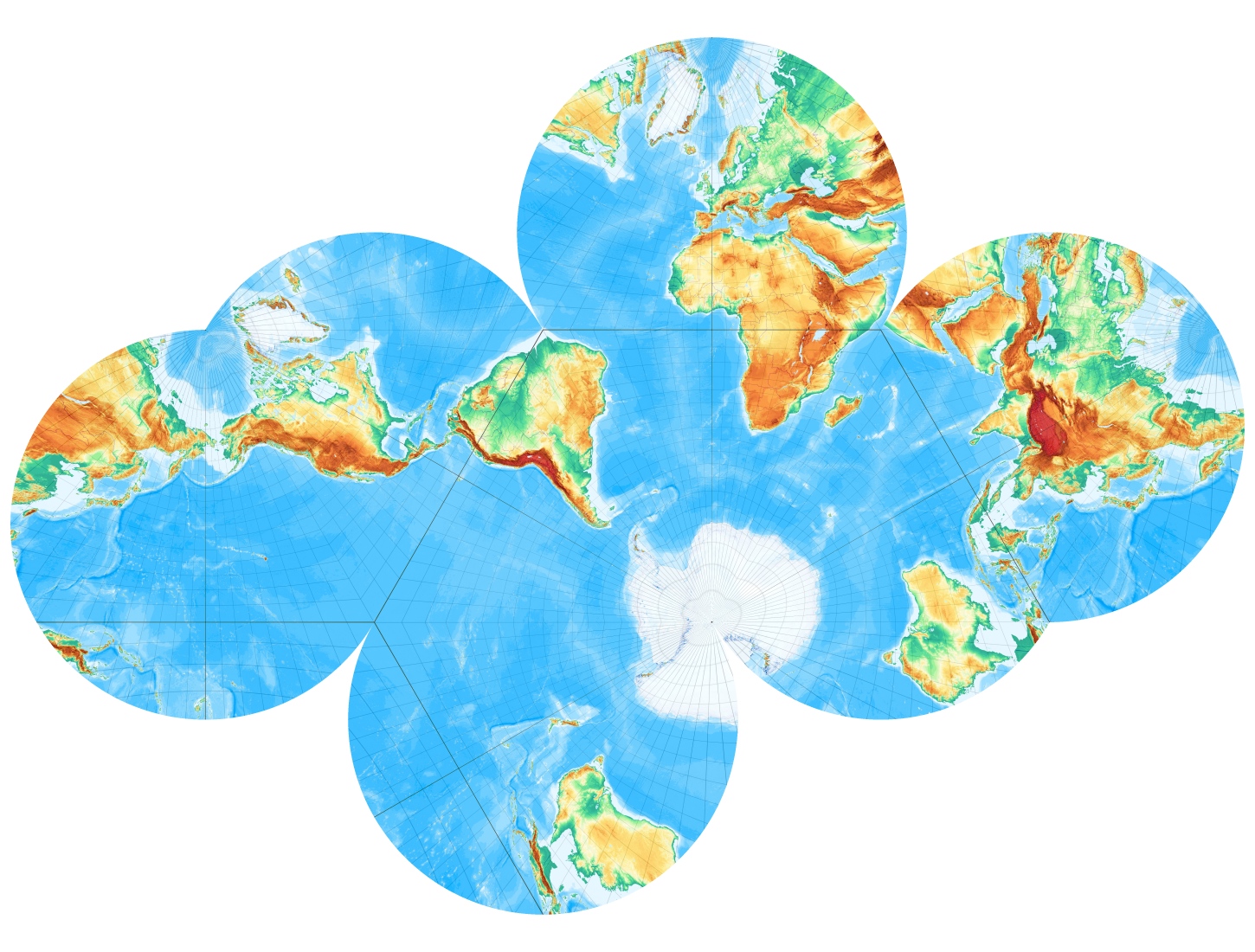
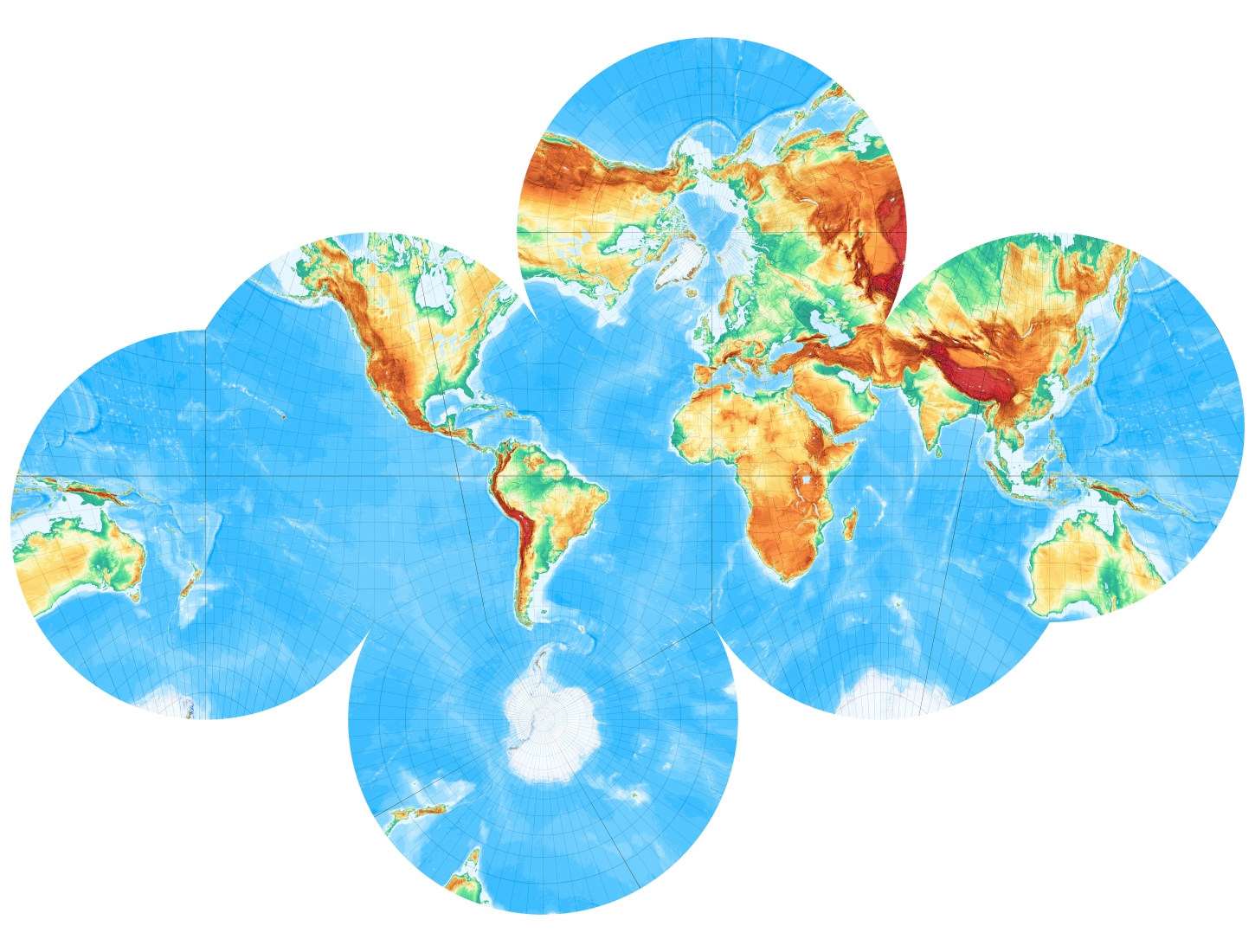
Man kann auch den Pol in eine Quadratmitte legen, was das Netz etwas vereinfacht („polare Lage“):

Das Verfahren lässt sich etwas verallgemeinern, indem man unsere Mutter Erde nicht nur auf den Würfel abbildet, sondern auf andere Körper, die von regelmäßigen Polygonen begrenzt werden – die fünf Platonischen Körper.

Die Erde im Oktaeder

Wenn man zwei quadratische („cheopspyramidenartige“) Pyramiden mit ihren Grundflächen zusammenklebt, entsteht das Oktaeder (Wikipedia). Das Oktaeder wird von 8 Dreiecken begrenzt:

Das Oktaeder in polarer Lage:

21.11.2016 Congratulations Good Design award receiving by Hajime Narukawa, Tokyo. May be, his world map it is founded on that projection in skew position.

Die Erde im Ikosaeder

Süd- und Nordpolargegend sind je eine Pyramide mit 5 Dreiecken als Seitenfläche und einem Fünfeck als Grundfläche. Diese werden durch einen „äquatorialen Gürtel“ aus 10 zickzackförmig angeordneten Dreiecken verbunden und – fertig ist das Ikosaeder (Wikipedia). Das Ikosaeder wird von 20 Dreiecken begrenzt:

Ikosaeder in polarer Lage:

Die Erde im Pentagon-Dodekaeder

Auch nicht allzu schwer: Man nehme zwei „fünfeckige Schüsseln“, die je ein Fünfeck als Boden und 5 Fünfecke als Seitenfläche haben. Diese lassen sich zum Pentagon-Dodekaeder (Wikipedia) zusammenfügen. Unser Dodekaeder wird also von 12 Fünfecken begrenzt:

>

Das Pentagon-Dodekaeder in polarer Lage:

Die Erde im Tetraeder

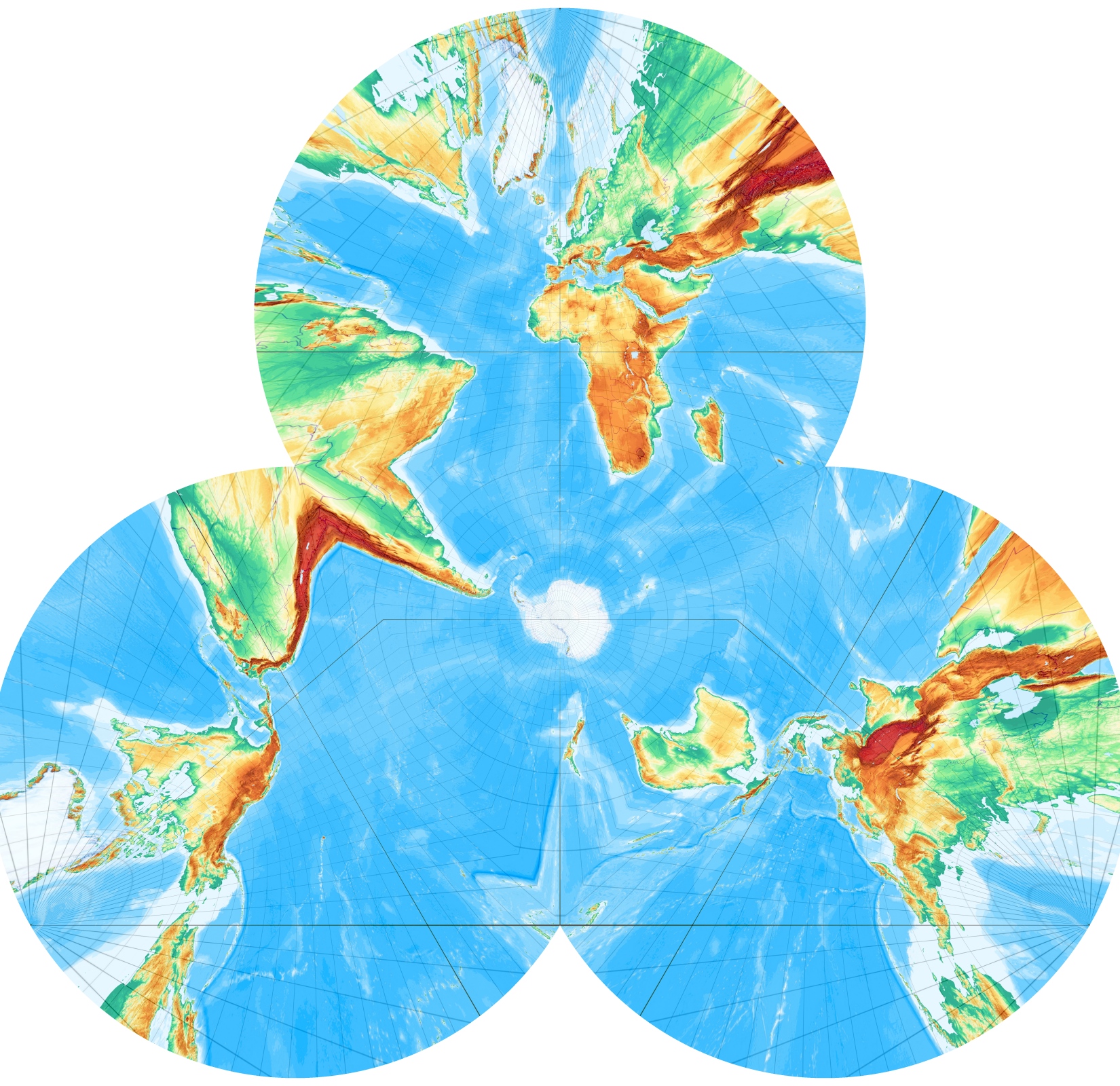
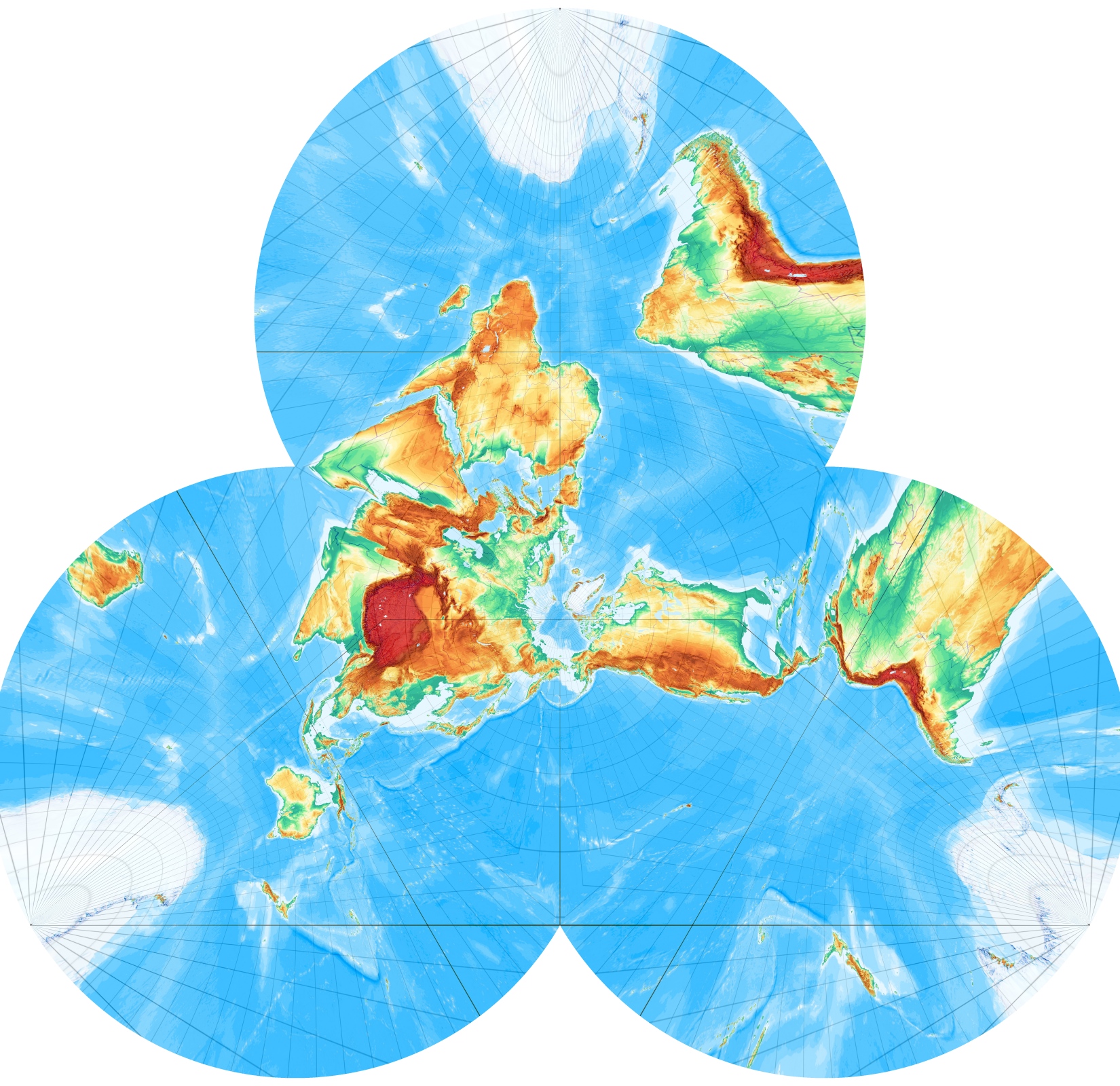
Ein Platonischer Körper fehlt noch, der allereinfachste: Das Tetraeder (Wikipedia), begrenzt von 4 Dreiecken. Weil die Umkugel des Tetraeders dreimal größer ist, als dessen Inkugel, geht der Graph „ganz schön aus dem Leim“ ... :

Umgekehrter Lage mit Nordpol als Flächenmittelpunkt, Südpol als Ecke:

Die Projektion, mit der die Polyeder gerechnet werden, ist die gnomonische Azimutalprojektion. Maßstab 1:400.000.000 bei 254 dpi. Die Programme normieren den Maßstab so, dass die Erde jeweils die Inkugel des betreffenden Polyeders bildet.

Kurze Skizze der softwaremäßigen Realisierung:

• Zunächst wird die Formel für die gnomonische Azimiutalprojektion in schiefachsiger (freier) Lage vorausgesetzt.
• Nun gibt es 3 Freiheitsgrade, die aus allen möglichen schiefachsigen gnomonischen Azimutalprojektionen genau eine bestimmte wählen: Die geographischen Koordinten λ und φ des Berührungspunktes, sowie eine Rotation. Hier werden für jedes Oberflächenpolygon des Polyeders 3 Werte in Tabellen gespeichert: FCCL, FCCP und FCCR („Face Center Lambda“, „Face Center Phi“, „Face Center Rotation“).
• Außerdem müssen die einzelnen Polygonflächen auf der Kartenebene (also „auf dem Bastelbogen“) angeordnet werden. Dazu wird jedes Oberflächenpolygon um eine bestimmte Verschiebungsstrecke versetzt. Hierzu gibt es 2 weitere Tabellen mit der Verschiebung X/Y, FCSX und FCSY („Face Shift X“, „Face Shift Y“).
• Nun ist für jede (einlaufende) Kartenkoordinate das zugehörige Polygon festzustellen. Es wird dasjenige Polygon i gewählt, bei dem die (euklidische) Entfernung zwischen zugehörigem Erdpunkt und tabellierter Polygonmitte (FCCL(i), FCCP(i)) minimal ist.
• Formeln: Zur Ermittlung der tabellierten Werte sind zunächst Dreieckshöhe (½√3) und Fünfecksdiagonale (½(√5+1)) wichtig. Die Formeln für die Inkugelradien der jeweiligen Platonischen Körper stehen in der Wikipedia, ebenso die ebenfalls benutzten Formeln zur Ermittlung Flächen-Flächen-Winkel, mit denen man von einer Seitenfläche zu deren Nachbarin voranschreiten kann. Die Ermittlung der Lagen der Flächen ist nicht immer ganz trivial (insbesondere bei Ikosaeder und Doedekaeder). Siehe hier den Kommentar im RTA-Programmtext.

[Die gnomonische Azimutalprojektion ist Entwurf 14b nach Wagner]

Assemblerprogramme:

Tetraeder
Tetraeder (polar)
Würfel
Würfel (polar)
Oktaeder
Oktaeder (polar)
Ikosaeder
Ikosaeder (polar)
Pentakondodekaeder
Pentakondodekaeder (polar)

17.03.2021: Kartenreihe World 1:100.000.000 (W100)