Redaktionsakte

Teil 4: Dokumentation SVG-Path-Element

Teil 1: Meine Kartensignaturensammlung
Teil 2: Meine Wegemarkensammlung
Teil 3: Wie ich meine Kartensignaturen in SVG definiere
Teil 4: Dokumentation SVG-Path-Element (Diese Seite)

Straßenschilder
Das Trekkingpfadzeichen
Über das große ẞ
Terrainkurwege Kurort Rathen

Wie haben die eigentlich früher Kartensignaturen hergestellt?

Die Originalsignatur befand sich auf einer kleinen Messingschablone. Die Schablone wurde mit einem kleinen chromblitzenden Gerät, dem Gravierpantografen, abgetastet und von einer feinen, nur 0,1 mm starken Nadel in eine Folienschicht graviert.

Kartensignaturen bloß nicht mit Riesensoftware machen. Viel zu kompliziert. Eine Handvoll minimalistische Zeichenbefehle, die es „auf den Punkt bringen“, reichen völlig aus. Und es gibt ein genialisches Format, das solche Zeichenbefehle realisiert, und das völlig ohne Plug-in auf jedem Browser läuft – SVG mit dem SVG-Element <path>, und hier insbesondere das ARC-Kommando in seiner endpoint parametrization. Eine Art perpetuum mobile kartographischen Signaturengestaltens? Könnte man so sagen.

Hier die detaillierte Beschreibung dieses Wunderwerkes:

Das SVG-path-Element

Das SVG-Path-Element beschreibt einen Linienzug – den Weg eines Zeichenstiftes. Es wird wie folgt notiert::

<path  data="pathdata"  stroke="col"  stroke-width="num"  fill="col">

Gezeichnet wird mit einer Linienfarbe col, in einer Linienstärke num, gelegentlich kann eine Füllfarbe col hinzutreten. Das eigentlich Geniale sind die Zeichenbefehle, die als <pathdata>-Zeichenkette im <data>-Attribut mitgeteilt werden. Minimal und mächtig: Diese Zeichenkette besteht aus einbuchstabigen Befehlen, denen (durch Leerzeichen oder Komma getrennt) Zahlenparameter folgen können. Diese geben meist Koordinaten an, manchmal auch einen Winkel in Grad oder Ja-Nein-Informationen („Flags“). Zu Beginn der Zeichnung wird der Zeichenstift auf eine „aktuellen Position“ oder „Cursorkoordinate“ gesetzt, was in der Regel mit einem M-Befehl erfolgt. Von dort aus wird dann gezeichnet. Es gibt lediglich 10 Befehle. Diese sind völlig ausreichend. Die Befehle sind:

   M x y           Moveto:                   Cursor auf Position x,y setzen
   L x y           Lineto:                   Linie von Corsorposition nach x,y zeichen
   H x             Horizontal lineto:        Horizontale Linie nach x zeichen
   V y             Vertical lineto:          Vertikale Linie nach y zeichen
   C s t u v x y   Cubic bézier:             Kubische Bézierkurve vom Cursor über r,s und u,v nach x,y
   Q s t x y       Quadratic bézier:         Quadratische Bézierkurve vom Cursor über r,s nach x,y
   S s t x y       Smooth cubic bézier:      Glatte kubische Bézierkurve über r,s nach x,y
   T x y           smooTh quadratic bézier:  Glatte quadratische Bézierkurve nach x,y
   A r s a i j x y Arc:                      Ellipsenbogen mit Halbachsen r,s, Winkellage s, Flags i/j nach x,y
   Z               cloZe path:               Linienzug schließen, indem zum Linienstartpunkt gezeichnet wird.
   R ...           catmull-Rom:              reserviert
   B ...           Bearing:                  reserviert
  

Hinten stehen immer die Koordinaten des Zielpunktes. Mit diesen Befehlen lassen sich praktisch alle Kartensignaturen erzeugen. Die Koordinaten sind grundsätzlich Absolutkoordinaten. Das ist dann der Fall, wenn Befehlsbuchstabe groß ist. Der Befehl M 120 -10 setzt z. B. den Cursor auf Position 120,-10. Wenn man die Befehle in Kleinbuchstaben notiert, so werden die Koordinaten zu Relativwerten. Der Befehl m 120 -10 versetzt z. B. den Cursor um 120 Koordinateneinheiten nach rechts und um 10 Einheiten nach unten.

2015 wurden noch 2 weitere Befehle vorgeschlagen, R für Catmull-Rom-Splines und B für eine Koordintensystemdrehung um einen Winkel in Grad. Diese haben sich jedoch nicht durchgesetzt, wurden wieder aus dem Standard herausgenommen und sind lediglich reserviert.

Bézierkurven

Die kubische Bézierkurve verläuft vom Cursor (I) über die beiden Steuerpunkte II und III zum Zielpunkt IV:

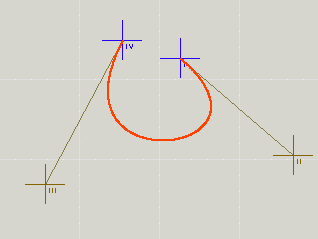
Bei der quadratischen Bézierkurve gibt es insgesamt nur 3 Punkte, der Linienzug verläuft vom Cursor (I) über einen Steuerpunkt II zum Zielpunkt III:

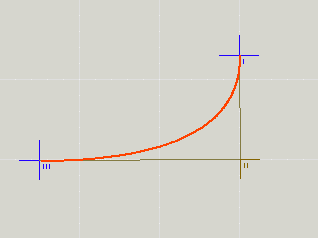
Die Smooth-Bezierkurven funktionieren wie die regulären Bézierkurven. Hierbei werden allerdings Steuerpunkte einer im Linienzug vorangegangenen Bézierkurve genutzt, um Neu-Steuerpunkte zu erzeugen. Die alten Steuerpunkte werden einfach um 180° gespiegelt „nach vorn geklappt“. So entsteht immer ein knickfrei geglätteter Linienzug. Das ist praktisch immer graphisch vorteilhaft.

Ellipsenbögen

Von besonderer Mächtigkeit ist der ARC-Befehl des path-Elements. Er zeichnet beliebige Kreise und Ellipsenbögen. Wesentlich ist sog. „endpoint parametrization“. Dies erspart dem Zeichner, den Mittelpunkt des Kreises oder der Ellipse zu kennen. — Nun also einen Ellipsenbogen zeichnen. Startpunkt und Endpunkt sind bekannt. Weiterhin, dass beide durch einen Ellipsenbogen miteinander verbunden werden sollen. Dafür gibt es unendlich viele Möglichkeiten. Genau genommen gibt es in der Ebene „4×Unendlich hoch 3“ mögliche Ellipsenbögen, welche 2 Punkte miteinander verbinden. Um hieraus einen einzigen bestimmten Bogen auszuwählen, müssen diese 3 Freiheitsgrade durch die Angabe von 3 Zahlenwerten „gehoben werden“. Der ARC-Befehl macht dies mit folgenden Angaben:

1. Kleine Halbachse r
2. Große Halbachse s
3. Winkel zwischen großer Halbachse und X-Achse a

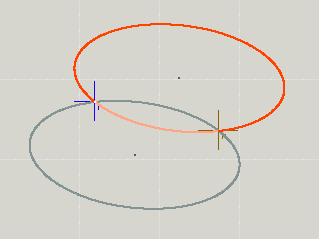
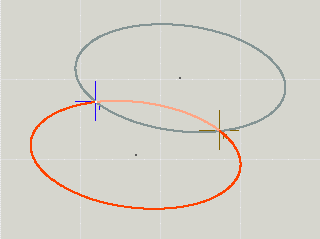
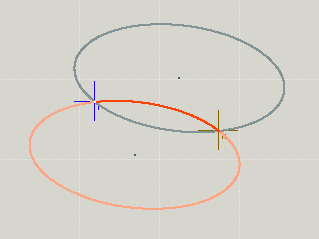
Um die richtige Lösung auszuwählen, werden zwei Flags i und j (das „Large-Arc-Flag“ und „Sweep-Flag“) genutzt. Diese können jeweils 0 oder 1 sein. Die 4 Möglichkeiten 0/0, 0/1, 1/0 und 1/1 wählen genau die passende Lösung aus.

Wenn die Halbachsen kleiner werden, rücken die Ellipsenmittelpunkte immer weiter zusammen:

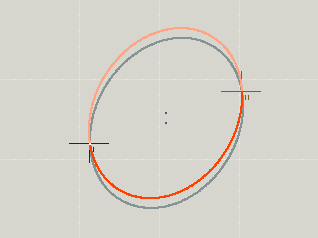
Wenn die Halbachsen zu klein werden, gibt schließlich keine Ellipse mehr, die die beiden Punkte zu verbinden in der Lage wäre. In diesen Fällen werden beide Halbachsen mit einem Faktor λ multipliziert, der ihr Verhältnis wahrt und sie gerade auf minimale Länge bringt:

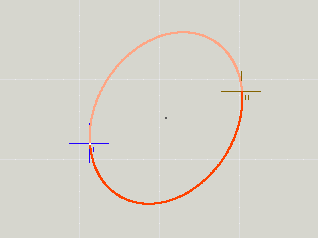
Dies lässt sich raffiniert ausnutzen, um zwei Punkte mit einem 180°-Bogen zu verbinden. Um vom Cursor z. B. mit einem Halbkreis Punkt 300,150 zu erreichen, notiere man einfach A 1 1 0 0 0 300 150

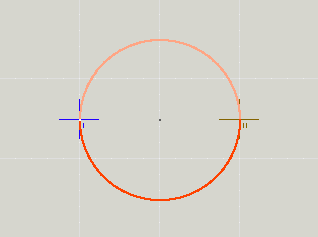
Die beiden Halbmesser 1 und 1 werden dank λ geeignet vergrößert, der Winkel ist im Kreisfall uninteressant, einzig das Sweep-Flag muss ggf. durch Ausprobieren passend auf 0 oder 1 gesetzt werden.

Anmerkung: Die Formeln, mit denen man die „endpoint parametrization“ in eine „centerpoint parametrization“ umwandelt, sind hier nachzulesen. (http://www.w3.org/TR/2003/REC-SVG11-20030114/implnote.html)

Nicht soviel Theorie ...

Nun bitte ein praktisches Beispiel

Mit diesem Code wird eine Denksteinsignatur erzeugt:

<!-- DENKSTEIN -->
<!-- ========= -->
<!-- FUELLUNG -->
<path d=
  "
    M -50,0
    L -50,125
    A 50 50 0 0 0 50,125
    L 50,0
    L -50,0
  "
  stroke-width="1" stroke="black" fill="#fcfcfc" zx="0" zy="50"
/>
<!-- UMRISS -->
<path d=
  "
    M -120,0
    L 150,0
    L -50,0
    L -50,125
    A 50 50 0 0 0 50,125
    L 50,0
    M -50,125
    A 57.5 57.5 0 0 0 65,125
    L 65,0
    M -50,125
    A 65 65 0 0 0 80,125
    L 80,0
  "
  stroke-width="20" stroke="black"
/>
  

Und nun bitte ausplotten

Es entsteht folgendes Bild:

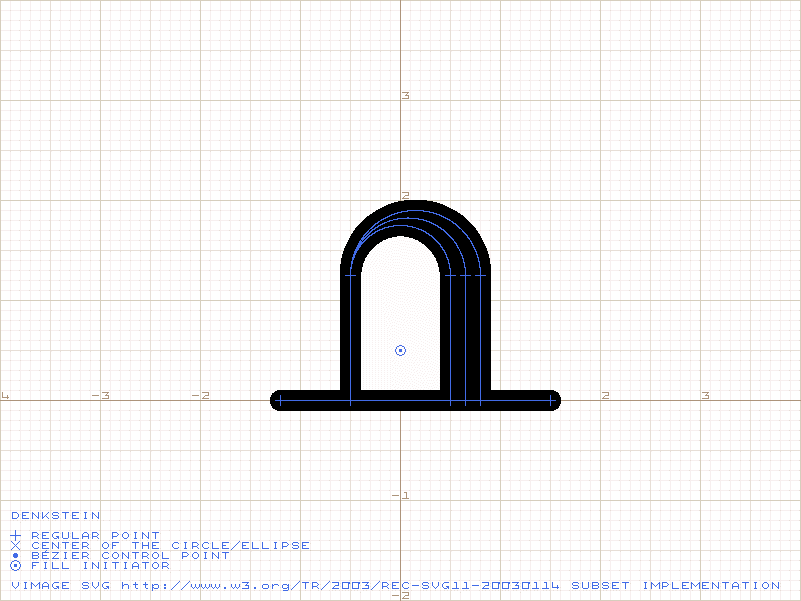
Nicht schlecht oder?

Siehe auch hier hier.

27.02.2017 aktualisiert
12.04.2023 aktualisiert